题目内容
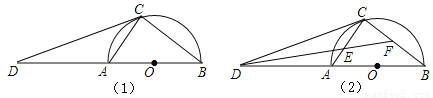
如图(1)，AB为半圆O的直径，D为BA的延长线上一点，DC为半圆O的切线，切点为C．
（1）求证：∠ACD=∠B；
（2）如图(2)，∠BDC的平分线分别交AC，BC于点E，F，求∠CEF的度数．
练习册系列答案
快乐5加2金卷系列答案
相关题目
快乐5加2金卷系列答案题目内容
如图(1)，AB为半圆O的直径，D为BA的延长线上一点，DC为半圆O的切线，切点为C．
（1）求证：∠ACD=∠B；
（2）如图(2)，∠BDC的平分线分别交AC，BC于点E，F，求∠CEF的度数．
快乐5加2金卷系列答案
（公式里的
，
B. 
D. 
B. 
C. 
D. 
，其中x2+2x﹣1=0．
(
