题目内容
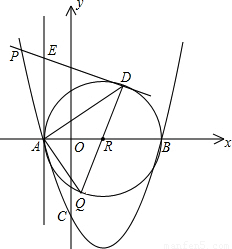
 如图,抛物线与坐标轴分别交于点A(a,0),B(b,0),C(0,c),其中abc=9,a、b、c均为整数,且a<0,b>0,c<0,|a|<|b|=|c|,以AB为直径作圆R,过抛物线上一点P作直线PD切圆R于D,并与圆R的切线AE交于点E,连接DR并延长交圆R于点Q,连接AQ,AD.
如图,抛物线与坐标轴分别交于点A(a,0),B(b,0),C(0,c),其中abc=9,a、b、c均为整数,且a<0,b>0,c<0,|a|<|b|=|c|,以AB为直径作圆R,过抛物线上一点P作直线PD切圆R于D,并与圆R的切线AE交于点E,连接DR并延长交圆R于点Q,连接AQ,AD.(1)求抛物线所对应的函数关系式;
(2)若四边形EARD的面积为4
| 3 |
(3)抛物线上是否存在点P,使得四边形EARD的面积等于△DAQ的面积?若存在,求出P点的坐标;若不存在,说明理由.
分析:(1)根据abc=9,a、b、c均为整数,且a<0,b>0,c<0,|a|<|b|=|c|,得出A、B、C的坐标即可用待定系数法求出抛物线的解析式,进而可用配方法求出其顶点坐标;
(2)连接ER,过D作DF⊥x轴于F;由于ED、EA都是⊙O的切线,根据切线长定理可得EA=ED,易证得△EAR≌△EDR则它们的面积相等,由此可得到S△EAR=2
,即可求出EA的长,也就得到了E点的坐标;在Rt△EAR中,根据EA、AR的值,即可求出∠ERA的度数,进而可求出∠DRF的度,从而在Rt△DRF中,通过解直角三角形求出RF、DF的长,由此求得D点坐标,用待定系数法即可求出直线DP的解析式;(需注意的是AE的长为正值,但是E点的纵坐标有正负两种情况,所以要分类讨论)
(3)在△DAQ中,由于DQ是⊙M的直径,所以DR=QR,则△DAR和△RAQ等底同高,所以面积相等,即△DAQ的面积是△DAR的2倍;在(2)题中已经求出四边形EARD的面积是△EAR的2倍,若四边形EARD的面积等于△DAQ的面积,则△DAR、△EAR的面积相等,这两个三角形共用底边AR,所以它们的高相同,由此可证得PD与x轴平行,即PD的解析式为y=±2,联立抛物线的解析式即可求出P点的坐标.
(2)连接ER,过D作DF⊥x轴于F;由于ED、EA都是⊙O的切线,根据切线长定理可得EA=ED,易证得△EAR≌△EDR则它们的面积相等,由此可得到S△EAR=2
| 3 |
(3)在△DAQ中,由于DQ是⊙M的直径,所以DR=QR,则△DAR和△RAQ等底同高,所以面积相等,即△DAQ的面积是△DAR的2倍;在(2)题中已经求出四边形EARD的面积是△EAR的2倍,若四边形EARD的面积等于△DAQ的面积,则△DAR、△EAR的面积相等,这两个三角形共用底边AR,所以它们的高相同,由此可证得PD与x轴平行,即PD的解析式为y=±2,联立抛物线的解析式即可求出P点的坐标.
解答: 解:(1)∵抛物线与坐标轴分别交于点A(a,0),B(b,0),C(0,c),其中abc=9,a、b、c均为整数,且a<0,b>0,c<0,|a|<|b|=|c|,
解:(1)∵抛物线与坐标轴分别交于点A(a,0),B(b,0),C(0,c),其中abc=9,a、b、c均为整数,且a<0,b>0,c<0,|a|<|b|=|c|,
∴b,c互为相反数,|b|=|c|≤3,
∴b=3,c=-3,a=-1,
所以抛物线与x轴交于点A(-1,0)、B(3,0)两点,
设抛物线的函数关系式为:y=a(x+1)(x-3),
∵抛物线与y轴交于点C(0,-3),
∴-3=a(0+1)(0-3),
∴a=1,
所以,抛物线的函数关系式为:y=x2-2x-3,
又∵y=(x-1)2-4,
因此,抛物线的顶点坐标为(1,-4);
(2)连接ER,∵EA、ED是⊙R的两条切线,
∴EA=ED,EA⊥AR,ED⊥RD,
在Rt△EAR和Rt△EDR中,
,
∴△EAR≌△EDR(HL),
又∵四边形EARD的面积为4
,
∴S△EAR=2
,
∴
AR•AE=2
,
又∵AR=2,
∴AE=2
,
因此,点E的坐标为E1(-1,2
)或E2(-1,-2
),
当E点在第二象限时,切点D在第一象限,
在直角三角形EAR中,tan∠ERA=
=
=
,
∴∠ERA=60°,
∴∠DRB=60°,
过切点D作DF⊥AB,垂足为点F,
∴RF=1,DF=
,
因此,切点D的坐标为(2,
),
设直线PD的函数关系式为y=kx+b,
将E(-1,2
),D(2,
)的坐标代入得,
,
解之,得:
,
所以,直线PD的函数关系式为:y=-
x+
,
当E点在第三象限时,切点D在第四象限,
同理可求:切点D坐标为(2,-
),
直线PD的函数关系式为y=
x-
,
因此,直线PD的函数关系式为y=-
x+
或y=
x-
;
(3)若四边形EARD的面积等于△DAQ的面积,
又∵S四边形EARD=2S△EAR,S△DAQ=2S△ARD,
∴S△ARD=S△EAR,
∴E、D两点到x轴的距离相等,
∵PD与⊙R相切,
∴点D与点E在x轴同侧,
∴切线PD与x轴平行,
此时切线PD的函数关系式为y=2或y=-2,
当y=2时,由y=x2-2x-3得,x=1±
;
当y=-2时,由y=x2-2x-3得,x=1±
,
故满足条件的点P的位置有4个,分别是P1(1+
,2)、P2(1-
,2)、P3(1+
,-2)、P4(1-
,-2).
 解:(1)∵抛物线与坐标轴分别交于点A(a,0),B(b,0),C(0,c),其中abc=9,a、b、c均为整数,且a<0,b>0,c<0,|a|<|b|=|c|,
解:(1)∵抛物线与坐标轴分别交于点A(a,0),B(b,0),C(0,c),其中abc=9,a、b、c均为整数,且a<0,b>0,c<0,|a|<|b|=|c|,∴b,c互为相反数,|b|=|c|≤3,
∴b=3,c=-3,a=-1,
所以抛物线与x轴交于点A(-1,0)、B(3,0)两点,
设抛物线的函数关系式为:y=a(x+1)(x-3),
∵抛物线与y轴交于点C(0,-3),
∴-3=a(0+1)(0-3),
∴a=1,
所以,抛物线的函数关系式为:y=x2-2x-3,
又∵y=(x-1)2-4,
因此,抛物线的顶点坐标为(1,-4);
(2)连接ER,∵EA、ED是⊙R的两条切线,
∴EA=ED,EA⊥AR,ED⊥RD,
在Rt△EAR和Rt△EDR中,
|
∴△EAR≌△EDR(HL),
又∵四边形EARD的面积为4
| 3 |
∴S△EAR=2
| 3 |
∴
| 1 |
| 2 |
| 3 |
又∵AR=2,
∴AE=2
| 3 |
因此,点E的坐标为E1(-1,2
| 3 |
| 3 |
当E点在第二象限时,切点D在第一象限,
在直角三角形EAR中,tan∠ERA=
| AE |
| AR |
2
| ||
| 2 |
| 3 |
∴∠ERA=60°,
∴∠DRB=60°,
过切点D作DF⊥AB,垂足为点F,
∴RF=1,DF=
| 3 |
因此,切点D的坐标为(2,
| 3 |
设直线PD的函数关系式为y=kx+b,
将E(-1,2
| 3 |
| 3 |
|
解之,得:
|
所以,直线PD的函数关系式为:y=-
| ||
| 3 |
5
| ||
| 3 |
当E点在第三象限时,切点D在第四象限,
同理可求:切点D坐标为(2,-
| 3 |
直线PD的函数关系式为y=
| ||
| 3 |
5
| ||
| 3 |
因此,直线PD的函数关系式为y=-
| ||
| 3 |
5
| ||
| 3 |
| ||
| 3 |
5
| ||
| 3 |
(3)若四边形EARD的面积等于△DAQ的面积,
又∵S四边形EARD=2S△EAR,S△DAQ=2S△ARD,
∴S△ARD=S△EAR,
∴E、D两点到x轴的距离相等,
∵PD与⊙R相切,
∴点D与点E在x轴同侧,
∴切线PD与x轴平行,
此时切线PD的函数关系式为y=2或y=-2,
当y=2时,由y=x2-2x-3得,x=1±
| 6 |
当y=-2时,由y=x2-2x-3得,x=1±
| 2 |
故满足条件的点P的位置有4个,分别是P1(1+
| 6 |
| 6 |
| 2 |
| 2 |
点评:此题主要考查了二次函数解析式的确定、切线的性质、切线长定理、全等三角形的判定和性质、图形面积的求法等重要知识,同时还考查了分类讨论的数学思想,综合性强,难度较大.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
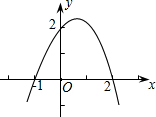 如图,抛物线与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则当y>2时,自变量x的取值范围是( )
如图,抛物线与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则当y>2时,自变量x的取值范围是( )A、0<x<
| ||
| B、0<x<1 | ||
C、
| ||
| D、-1<x<2 |
 =-1,与x轴交于点C,且∠ABC=90°
=-1,与x轴交于点C,且∠ABC=90°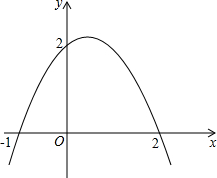 (2012•翔安区模拟)如图,抛物线与两坐标轴的交点坐标分别为(-1,0),(2,0),(0,2),
(2012•翔安区模拟)如图,抛物线与两坐标轴的交点坐标分别为(-1,0),(2,0),(0,2), ,求直线PD的函数关系式;
,求直线PD的函数关系式;