Question

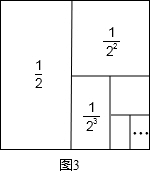
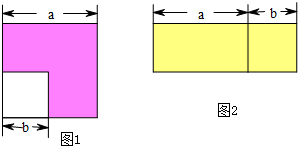如图1所示，边长为a的大正方形中有一个边长为b的小正方形，如图2是由图1中阴影部分拼成的一个长方形．
（1）请分别表示出这两个图形中阴影部分的面积______，______；
（2）以上结果可以验证那个乘法公式？______；
（3）试利用这个公式计算：2013²-2014×2012．

Answer 1

解：（1）大正方形的面积为a²，小正方形的面积为b²，
故图1阴影部分的面积值为a²-b²；
长方形的长和宽分别为（a+b）、（a-b），
故重拼的长方形的面积为（a+b）（a-b）；
（2）比较上面的结果，都表示同一阴影的面积，它们相等，
即a²-b²=（a+b）（a-b），可以验证平方差公式，这也是平方差公式的几何意义；
（3）2013²-2014×2012
=2013²-（2013+1）（2013-1）
=2013²-（2013²-1）
=2013²-2013²+1
=1．
分析：（1）求出大正方形及小正方形的面积，作差即可得出阴影部分的面积；图2所示的长方形的长和宽分别为（a+b）、（a-b），由此可计算出面积；
（2）根据阴影部分的面积相等可得出平方差公式；
（3）利用平方差公式计算即可．
点评：本题考查了平方差公式的几何背景，注意几次分割后边的变化情况是关键，属于基础题．