Question

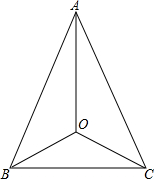如图，已知∠OBA=∠OCA，OB=OC．求证：AO平分∠BAC．

Answer 1

证明：∵OB=OC，
∴∠OBC=∠OCB，
∵∠OBA=∠OCA，
∴∠OBC+∠OBA=∠OCB+∠OCA，
∴∠ABC=∠ACB，
∴AB=AC，
在△ABO和△ACO中，
，
∴△ABO≌△ACO（SSS），
∴∠BAO=∠CAO，
即AO平分∠BAC．
分析：根据等边对等角得出∠OBC=∠OCB，求出∠ABC=∠ACB，推出AB=AC，证△ABO≌△ACO，推出∠BAO=∠CAO即可．
点评：本题考查了等腰三角形的性质和判定，全等三角形的性质和判定的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS．全等三角形的对应边相等，对应角相等．