题目内容

如图△ABC中M为BC的中点，N为AM上一点，过N作直线PQ分别交线段AB、AC于P、Q．
（1）当PQ∥BC时，求证：PN=NQ；
（2）当PQ与BC不平行时， $数学公式$ =______ $数学公式$ ．填空并证明．

解：（1）∵PQ∥BC，∴△APN∽△ABM，
∴ $\text{[math]}$ = $\text{[math]}$ ，
同理 $\text{[math]}$ = $\text{[math]}$ ，
∵BM=CM，∴PN=NQ

（2） $\text{[math]}$ =2 $\text{[math]}$ ，
如图，过B，C两点作AM的平行线交直线于D，F，
∵BD∥AM，CE∥AM
∴BD∥CE
∴△BDP∽△ANP，△CEQ∽△ANQ
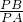∴ $\text{[math]}$ = $\text{[math]}$ ， $\text{[math]}$ = $\text{[math]}$ ，
∵M为BC的中点，MN∥CE∥BD
∴NM为梯形BDEC的中位线，
∴BD+EC=2MN，
∴ $\text{[math]}$ =2 $\text{[math]}$ ．
故答案为2．
分析：（1）由平行，可证得，△APN∽△ABM，则 $\text{[math]}$ = $\text{[math]}$ ，同理 $\text{[math]}$ = $\text{[math]}$ ，从而得出PN=NQ；
（2）分别过B，C两点作AM的平行线交直线于D，F，根据平行线段分线段成比例可证 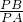$\text{[math]}$ = $\text{[math]}$ ， $\text{[math]}$ = $\text{[math]}$ ，再证NM为梯形BDEC的中位线，根据梯形的中位线原理可知BD+EC=2MN，从而得出结论．
点评：本题主要考查相似三角形的判定，梯形的中位线原理，平行线平分线段成比例几个考点，熟练掌握上述定理并灵活运用是解答本题的关键．