Question

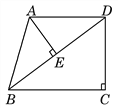
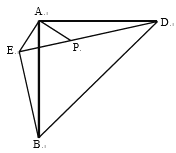
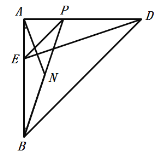
【题目】如图，为边长不变的等腰直角三角形，，，在外取一点，以为直角顶点作等腰直角，其中在内部，，，当E、P、D三点共线时，．

下列结论：

①E、P、D共线时，点到直线的距离为；

②E、P、D共线时，；

；

④作点关于的对称点，在绕点旋转的过程中，的最小值为；

⑤绕点旋转,当点落在上，当点落在上时，取上一点，使得，连接，则．

其中正确结论的序号是___．

Answer 1

【答案】②③⑤

【解析】

①先证得，利用邻补角和等腰直角三角形的性质求得，利用勾股定理求出，即可求得点到直线的距离；

②根据①的结论，利用即可求得结论；

③在中，利用勾股定理求得，再利用三角形面积公式即可求得；

④当共线时，最小，利用对称的性质，的长，再求得的长，即可求得结论；

⑤先证得，得到，根据条件得到，利用互余的关系即可证得结论．

①∵与都是等腰直角三角形，

∴，，，，，

∴，

∴，

∴，

∴，

∴，

∵，，

∴，

∴，

解得：，

作BH⊥AE交AE的延长线于点H，

∵，，

∴，

∴，

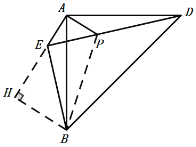
∴点到直线的距离为，故①错误；

②由①知：，，，

∴

，故②正确；

③在中，由①知：，

∴，

，

，故③正确；

④因为是定值，所以当共线时，最小，如图，连接BC，

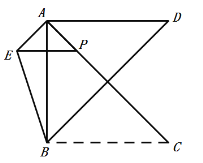
∵关于的对称，

∴，

∴，

∴ ，

，故④错误；

⑤∵与都是等腰直角三角形，

∴，，，，

在和中，，

∴，

∴，

∵，

∴，

∴，

∵，

∴，

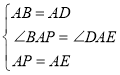∴，故⑤正确；

综上，②③⑤正确，

故答案为：②③⑤．