题目内容
1.一辆汽车的背面,有一种特殊形状的刮雨器,忽略刮雨器的宽度可抽象为一条折线OAB,如图1所示,量得连杆OA长为10cm,雨刮杆AB长为45cm,∠OAB=120°.若启动一次刮雨器,雨刮杆AB正好扫到水平线CD的位置,如图2所示.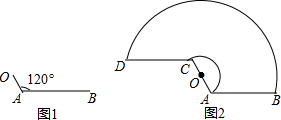
(1)求雨刮杆AB旋转的最大角度及O、B两点之间的距离;
(2)求雨刮杆AB扫过的最大面积.
分析 (1)利用已知图形得出雨刮杆AB旋转的最大角度,再利用锐角三角函数关系得出BE的长,进而求出BO的长;
(2)直接得出△BAO≌△OCD,进而得出雨刮杆AB扫过的最大面积.
解答 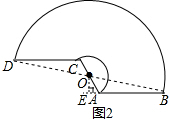 解:(1)雨刮杆AB旋转的最大角度为180°,
解:(1)雨刮杆AB旋转的最大角度为180°,
如图2,连接OB,过O点作AB的垂线交BA的延长线于E,
∵∠OAB=120°,∴∠OAE=60°
在Rt△OAE中,
∵∠OAE=60°,OA=10cm,
∴sin∠OAE=$\frac{OE}{OA}$=$\frac{OE}{10}$,
∴OE=5$\sqrt{3}$cm,AE=5cm
∴EB=AE+AB=50cm,
在Rt△OEB中,
∵OE=5$\sqrt{3}$cm,EB=50cm,
∴OB=$\sqrt{O{E^2}+B{E^2}}$=$\sqrt{2575}$=$5\sqrt{103}$(cm);
(2)∵雨刮杆AB旋转180°得到CD,即△OCD与△OAB关于点O中心对称,
∴△BAO≌△OCD,
∴S△BAO=S△OCD,
∴雨刮杆AB扫过的最大面积S=$\frac{1}{2}$π(OB2-OA2)=1237.5π(cm2).
点评 此题主要考查了勾股定理的应用以及锐角三角函数关系,利用锐角三角函数关系得出OE的长是解题关键.

练习册系列答案
相关题目
11.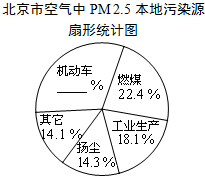 据报道,历经一年半的调查研究,北京PM2.5源解析已经通过专家论证.各种调查显示,机动车成为PM2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天就要向大气里排放0.035千克污染物.以下是相关的统计图表:
据报道,历经一年半的调查研究,北京PM2.5源解析已经通过专家论证.各种调查显示,机动车成为PM2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天就要向大气里排放0.035千克污染物.以下是相关的统计图表:
2014年北京市全年空气质量等级天数统计表
(1)请根据所给信息补全扇形统计图;
(2)请你根据“2014年北京市全年空气质量等级天数统计表”计算该年度重度污染和严重污染出现的频率共是多少?(精确到0.01)
(3)小明是社区环保志愿者,他和同学们调查了本社区的100辆机动车,了解到其中每天出行超过20千米的有40辆.已知北京市2014年机动车保有量已突破520万辆,请你通过计算,估计2014年北京市一天中出行超过20千米的机动车至少要向大气里排放多少千克污染物?
 据报道,历经一年半的调查研究,北京PM2.5源解析已经通过专家论证.各种调查显示,机动车成为PM2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天就要向大气里排放0.035千克污染物.以下是相关的统计图表:
据报道,历经一年半的调查研究,北京PM2.5源解析已经通过专家论证.各种调查显示,机动车成为PM2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天就要向大气里排放0.035千克污染物.以下是相关的统计图表:2014年北京市全年空气质量等级天数统计表
| 空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数(天) | 41 | 135 | 84 | 47 | 45 | 13 |
(2)请你根据“2014年北京市全年空气质量等级天数统计表”计算该年度重度污染和严重污染出现的频率共是多少?(精确到0.01)
(3)小明是社区环保志愿者,他和同学们调查了本社区的100辆机动车,了解到其中每天出行超过20千米的有40辆.已知北京市2014年机动车保有量已突破520万辆,请你通过计算,估计2014年北京市一天中出行超过20千米的机动车至少要向大气里排放多少千克污染物?
9.若$\sqrt{48n}$是正整数,最小的整数n是( )
| A. | 6 | B. | 3 | C. | 48 | D. | 2 |
6.参加一次商品交易会的每两家公司之间都签订了一份合同,所有公司共签订了45份合同.设共有x家公司参加商品交易会,则x满足的关系式为( )
| A. | $\frac{1}{2}$x(x+1)=45 | B. | $\frac{1}{2}$x(x-1)=45 | C. | x(x+1)=45 | D. | x(x-1)=45 |
13.点P(5,-3)关于原点的对称点是( )
| A. | (5,3) | B. | (-3,5) | C. | (-5,3) | D. | (3,-5) |
10.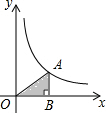 如图,在平面直角坐标系中,点A是双曲线y=$\frac{3}{x}$(x>0)上的一个动点,过点A作x轴的垂线,交x轴于点B,点A运动过程中△AOB的面积将会( )
如图,在平面直角坐标系中,点A是双曲线y=$\frac{3}{x}$(x>0)上的一个动点,过点A作x轴的垂线,交x轴于点B,点A运动过程中△AOB的面积将会( )
 如图,在平面直角坐标系中,点A是双曲线y=$\frac{3}{x}$(x>0)上的一个动点,过点A作x轴的垂线,交x轴于点B,点A运动过程中△AOB的面积将会( )
如图,在平面直角坐标系中,点A是双曲线y=$\frac{3}{x}$(x>0)上的一个动点,过点A作x轴的垂线,交x轴于点B,点A运动过程中△AOB的面积将会( )| A. | 逐渐增大 | B. | 逐渐减小 | C. | 先增大后减小 | D. | 不变 |