题目内容
设P为等腰直角△ABC斜边AB上或其延长线上一点,S=AP2+BP2,那么
- A.S<2CP2
- B.S=2CP2
- C.S>2CP2
- D.不确定
B
分析:此题分两种情况讨论:①当P在线段AB上,②当P在直线AB上(线段AB以外的部分);可利用勾股定理来探讨符合要求的点P有哪些.
解答: 解:当P为AB上时,假设P为中点时,AP=PB=PC,满足条件,
解:当P为AB上时,假设P为中点时,AP=PB=PC,满足条件,
当点P不为中点时,过点C作AB的垂线,亦满足条件;
当点P在BA的延长线上时,过点P作PF⊥BC,PE⊥CA;
PC2=PF2+CF2,AP2=AE2+PE2=AE2+FC2=2CF2
PB2=BF2+PF2=PF2+(BC+CF)2=2PF2
AP2+PB2=2CF2+PF2+PF2
2PC2=2PF2+2CF2
所以AP2+PB2=2PC2,
即S=2CP2;
同理,当点P在AB的延长线上时,S=2CP2.
综上可知:S=2CP2.
故选B.
点评:本题主要考查的是勾股定理的应用,解法并不复杂,难点在于将问题考虑全面.
分析:此题分两种情况讨论:①当P在线段AB上,②当P在直线AB上(线段AB以外的部分);可利用勾股定理来探讨符合要求的点P有哪些.
解答:
 解:当P为AB上时,假设P为中点时,AP=PB=PC,满足条件,
解:当P为AB上时,假设P为中点时,AP=PB=PC,满足条件,当点P不为中点时,过点C作AB的垂线,亦满足条件;
当点P在BA的延长线上时,过点P作PF⊥BC,PE⊥CA;
PC2=PF2+CF2,AP2=AE2+PE2=AE2+FC2=2CF2
PB2=BF2+PF2=PF2+(BC+CF)2=2PF2
AP2+PB2=2CF2+PF2+PF2
2PC2=2PF2+2CF2
所以AP2+PB2=2PC2,
即S=2CP2;
同理,当点P在AB的延长线上时,S=2CP2.
综上可知:S=2CP2.
故选B.
点评:本题主要考查的是勾股定理的应用,解法并不复杂,难点在于将问题考虑全面.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 20、设P为等腰直角三角形ACB斜边AB上任意一点,PE垂直AC于点E,PF垂直BC于点F,PG垂直EF于点G,延长GP并在其延长线上取一点D,使得PD=PC,试证:BC⊥BD,且BC=BD.
20、设P为等腰直角三角形ACB斜边AB上任意一点,PE垂直AC于点E,PF垂直BC于点F,PG垂直EF于点G,延长GP并在其延长线上取一点D,使得PD=PC,试证:BC⊥BD,且BC=BD.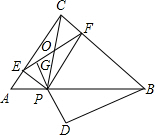 设P为等腰直角三角形ACB斜边AB上任意一点,PE垂直AC于点E,PF垂直BC于点F,PG垂直EF于点G,延长GP并在其延长线上取一点D,使得PD=PC,试证:BC⊥BD,且BC=BD.
设P为等腰直角三角形ACB斜边AB上任意一点,PE垂直AC于点E,PF垂直BC于点F,PG垂直EF于点G,延长GP并在其延长线上取一点D,使得PD=PC,试证:BC⊥BD,且BC=BD.