题目内容
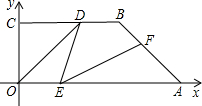
如图,直角梯形OABC中,AB∥OC,其中O(0,0),A(0,4| 3 |
| 3 |
 直BC于H,若OH=4
直BC于H,若OH=4| 3 |
(1)求∠HOC的度数;
(2)动点P从点O出发,沿线段OH向点H运动,动点Q从点A出发,沿线段AO向点O 运动,两点同时出发,速度都为每秒1个单位长度,设点P的运动时间为t秒.
①若直线QP交x轴的正半轴于点N,当t为何值时,QP=2PN;
②在P,Q的运动过程中,是否存在t值,使得△OPQ与△HOB相似,若存在,求出t的值;若不存在,请说明理由.
分析:(1)首先由三角函数,求得∠AOB的度数,由HL,可证得Rt△AOB≌Rt△HOB,即可求得∠HOC的度数;
(2)首先作辅助线:过点N与H作NK⊥x轴,即可得到相似三角形:△POQ∽△PKN,由相似三角形的对应边成比例,即可求得t的值;
(3)由相似三角形的判定,易得当QP⊥OH时,△OPQ∽△HOB,由三角函数的性质,即可求得当t=
时,△OPQ与△HOB相似.
(2)首先作辅助线:过点N与H作NK⊥x轴,即可得到相似三角形:△POQ∽△PKN,由相似三角形的对应边成比例,即可求得t的值;
(3)由相似三角形的判定,易得当QP⊥OH时,△OPQ∽△HOB,由三角函数的性质,即可求得当t=
4
| ||
| 3 |
解答:解:(1)∵OA=4
,AB=4,∠OAB=90°,
∴tan∠AOB=
=
,
∴∠AOB=30°,
∵OA=OH,OB=OB,∠BAO=∠BHO=90°,
∴Rt△AOB≌Rt△HOB(HL),
∴∠BOH=∠AOB=30°,
∴∠HOC=30°;
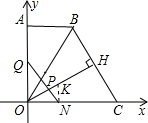
(2)①过点N与H作NK⊥x轴,
∴NK∥OA,
∴△POQ∽△PKN,
∴当
=
=
=
时,
∵OQ=4
-t,OP=t,
∴PK=
t,NK=
(4
-t),
∴OK=
t,
∵∠HOC=30°,
∴
=
=
=
,
∴t=
,
∴当t为
时,QP=2PN;
②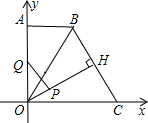 当QP⊥OH时,△OPQ∽△HOB.
当QP⊥OH时,△OPQ∽△HOB.
∵∠QPO=∠OHB=90°,∠QOP=∠OBH=60°,
∴△OPQ∽△HOB,
∴cos∠QOP=
=
=
,
∴t=
,
∴当t=
时,△OPQ与△HOB相似.
③当PQ⊥OA时,△OPQ∽△BOH,
cos∠QOP=
=
=
,
解得:t=
.
| 3 |
∴tan∠AOB=
| AB |
| OA |
| ||
| 3 |
∴∠AOB=30°,
∵OA=OH,OB=OB,∠BAO=∠BHO=90°,
∴Rt△AOB≌Rt△HOB(HL),
∴∠BOH=∠AOB=30°,
∴∠HOC=30°;

(2)①过点N与H作NK⊥x轴,
∴NK∥OA,
∴△POQ∽△PKN,
∴当
| NK |
| OQ |
| PK |
| OP |
| PN |
| PQ |
| 1 |
| 2 |
∵OQ=4
| 3 |
∴PK=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴OK=
| 3 |
| 2 |
∵∠HOC=30°,
∴
| NK |
| OK |
| ||||
|
4
| ||
| 3t |
| 1 |
| 2 |
∴t=
8
| ||
| 5 |
∴当t为
8
| ||
| 5 |
②
 当QP⊥OH时,△OPQ∽△HOB.
当QP⊥OH时,△OPQ∽△HOB.∵∠QPO=∠OHB=90°,∠QOP=∠OBH=60°,
∴△OPQ∽△HOB,
∴cos∠QOP=
| OP |
| OQ |
| t | ||
4
|
| 1 |
| 2 |
∴t=
4
| ||
| 3 |
∴当t=
4
| ||
| 3 |
③当PQ⊥OA时,△OPQ∽△BOH,
cos∠QOP=
| OQ |
| OP |
4
| ||
| t |
| 1 |
| 2 |
解得:t=
8
| ||
| 3 |
点评:此题考查了相似三角形的判定与性质,以及三角函数的性质与全等三角形的判定与性质.题目综合性很强,难度比较大,解题时要注意仔细分析求解.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目

 如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=
如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y= 如图,直角梯形OABC中,∠OAB=∠B=90°,A点在x轴上,双曲线y=
如图,直角梯形OABC中,∠OAB=∠B=90°,A点在x轴上,双曲线y=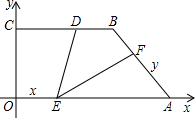 是BC上一点,BD=
是BC上一点,BD=