题目内容
6.如图1,已知点A(-1,-4)是二次函数y=ax2+bx-3(a≠0)的图象的顶点,且此二次函数的图象与x轴的负半轴相交于点B,与y轴相交于点C,点P是线段AB上任意一点,过点P的直线l与x轴垂直,垂足为D,且直线l与此二次函数的图象相交于点E.
(1)求此二次函数的解析式;
(2)求线段PE的长度的最大值;
(3)如图2,当线段PE的长度取最大值时,将直线l向右平移$\frac{1}{2}$个单位长度,平移后的直线称为直线l1,设点P1是直线l1与线段AB的交点,连接P1C,CD1.若△P2CD1与△P1CD1关于直线CD1对称,求点P2的坐标,并判断点P2是否在已知的二次函数的图象上.
分析 (1)设顶点式y=a(x+1)2-4,然后展开得到a-4=-3,则求出a即可得到抛物线解析式;
(2)如图1,先确定B(-3,0),C(0,-3),再利用待定系数法求出直线AB的解析式为y=-2x-6,则设E(x,x2+2x-3),则P(x,-2x-6),所以PE=-2x-6-(x2+2x-3)=-x2-4x-3,然后根据二次函数的性质解决问题;
(3)如图2,由(2)得到D(-2,0),则利用平移的性质得D1(-$\frac{3}{2}$,0),再求出P1(-$\frac{3}{2}$,-3),于是可判断P1C∥x轴,D1P1=3,所以P1C=$\frac{3}{2}$,接着利用对称的性质得P2D1=3,P2C=$\frac{3}{2}$,设P2(a,b),然后根据两点间的距离公式得到(a+$\frac{3}{2}$)2+b2=32,a2+(b+3)2=($\frac{3}{2}$)2,再解关于a、b的方程组即可得到点P2的坐标,于是可判断点P2是否在已知的二次函数的图象上.
解答 解:(1)设抛物线的解析式y=a(x+1)2-4,
即y=ax2+2ax+a-4,
∴a-4=-3,解得a=1,
∴抛物线解析式为y=x2+2x-3;
(2)如图1,
当y=0时,x2+2x-3=0,解得x1=-3,x2=1,则B(-3,0),
当x=0时,y=x2+2x-3=-3,则C(0,-3),
设直线AB的解析式为y=mx+n,
把B(-3,0),A(-1,-4)代入得$\left\{\begin{array}{l}{-3m+n=0}\\{-m+n=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-2}\\{n=-6}\end{array}\right.$,
∴直线AB的解析式为y=-2x-6,
设E(x,x2+2x-3),则P(x,-2x-6),
∵PE=-2x-6-(x2+2x-3)=-x2-4x-3=-(x+2)2+1,
∴当x=-2时,线段PE的最大值为1;
(3)如图2,
D(-2,0),
∵直线l向右平移$\frac{1}{2}$个单位长度,平移后的直线称为直线l1,
∴D1(-$\frac{3}{2}$,0),
当x=-$\frac{3}{2}$,y=-2x-6=-3,则P1(-$\frac{3}{2}$,-3),
而C(0,-3),
∴P1C∥x轴,D1P1=3,
∴P1C=$\frac{3}{2}$,
∵△P2CD1与△P1CD1关于直线CD1对称,
∴P2D1=3,P2C=$\frac{3}{2}$,
设P2(a,b),
∴(a+$\frac{3}{2}$)2+b2=32,a2+(b+3)2=($\frac{3}{2}$)2,解得a=$\frac{9}{10}$,b=-$\frac{9}{5}$或a=-$\frac{3}{2}$,b=-3,
∴P2点的坐标为($\frac{9}{10}$,-$\frac{9}{5}$),
当x=$\frac{9}{10}$时,y=($\frac{9}{10}$+1)2-4=-$\frac{39}{100}$,
∴点P2不在已知的二次函数的图象上.
点评 本题考查了二次函数的综合题:熟练掌握二次函数的图象上点的坐标特征.二次函数的性质和折叠的性质;会利用待定系数法求二次函数的解析式;理解坐标与图形性质,记住两点间的距离公式.

 快车与慢车分别从甲、乙两地同时出发,匀速相向而行,快车到达乙地后立刻返回,慢车到达甲地后停止行驶.途中折线表示从两车出发到慢车到达甲地过程中,两车间的距离y(km)与慢车行驶时间x(h)之间的函数关系,根据图中信息,有下列说法:①甲、乙两地相距400km;②快车速度是慢车速度的1.5倍;③快车从甲地到乙地共用了$\frac{10}{3}$小时;④点A的坐标为(5,200);其中符合图象描述的说法有( )
快车与慢车分别从甲、乙两地同时出发,匀速相向而行,快车到达乙地后立刻返回,慢车到达甲地后停止行驶.途中折线表示从两车出发到慢车到达甲地过程中,两车间的距离y(km)与慢车行驶时间x(h)之间的函数关系,根据图中信息,有下列说法:①甲、乙两地相距400km;②快车速度是慢车速度的1.5倍;③快车从甲地到乙地共用了$\frac{10}{3}$小时;④点A的坐标为(5,200);其中符合图象描述的说法有( ) 如图所示,?ABCD的顶点A、D在反比例函数$y=\frac{k}{x}$(k<0,x<0)的图象上,顶点B、C分别在坐标轴上.
如图所示,?ABCD的顶点A、D在反比例函数$y=\frac{k}{x}$(k<0,x<0)的图象上,顶点B、C分别在坐标轴上.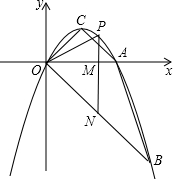 如图,抛物线y=ax2+bx经过A(2,0),B(3,-3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m.
如图,抛物线y=ax2+bx经过A(2,0),B(3,-3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m. 如图,已知⊙O的半径OA的长为2,点B是⊙O上的动点,以AB为半径的⊙A与线段OB相交于点C,AC的延长线与⊙O相交于点D.设线段AB的长为x,线段OC的长为y.
如图,已知⊙O的半径OA的长为2,点B是⊙O上的动点,以AB为半径的⊙A与线段OB相交于点C,AC的延长线与⊙O相交于点D.设线段AB的长为x,线段OC的长为y.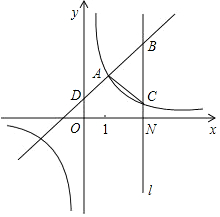 如图,一次函数y=x+b(b>0)与反比例函数y=$\frac{k}{x}$(k≠0)的图象有一个公共点A,直线l⊥x轴于点N(a,0),且与一次函数和反比例函数的图象分别交于点B,C.
如图,一次函数y=x+b(b>0)与反比例函数y=$\frac{k}{x}$(k≠0)的图象有一个公共点A,直线l⊥x轴于点N(a,0),且与一次函数和反比例函数的图象分别交于点B,C.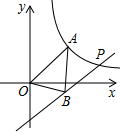 如图,反比例函数y=$\frac{k}{x}$的图象与直线y=x+m在第一象限交于点P(6,2),点A为反比例函数图象上的一点,作AB∥y轴,交直线y=x+m于点B,连结OA,OB.
如图,反比例函数y=$\frac{k}{x}$的图象与直线y=x+m在第一象限交于点P(6,2),点A为反比例函数图象上的一点,作AB∥y轴,交直线y=x+m于点B,连结OA,OB.