ЬтФПФкШн
ЁОЬтФПЁПдкСтаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧЩфЯп
ЪЧЩфЯп![]() ЩЯвЛЖЏЕуЃЌвд
ЩЯвЛЖЏЕуЃЌвд![]() ЮЊБпЯђгвВрзїЕШБп
ЮЊБпЯђгвВрзїЕШБп![]() ЃЌЕу
ЃЌЕу![]() ЕФЮЛжУЫцзХЕу
ЕФЮЛжУЫцзХЕу![]() ЕФЮЛжУБфЛЏЖјБфЛЏ.
ЕФЮЛжУБфЛЏЖјБфЛЏ.
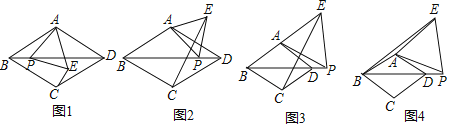
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕу![]() дкСтаЮ
дкСтаЮ![]() ФкВПЛђБпЩЯЪБЃЌСЌНг
ФкВПЛђБпЩЯЪБЃЌСЌНг![]() ЃЌ
ЃЌ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЪЧ______ЃЌ
ЕФЪ§СПЙиЯЕЪЧ______ЃЌ![]() гы
гы![]() ЕФЮЛжУЙиЯЕЪЧ______ЃЛ
ЕФЮЛжУЙиЯЕЪЧ______ЃЛ
ЃЈ2ЃЉЕБЕу![]() дкСтаЮ
дкСтаЮ![]() ЭтВПЪБЃЌЃЈ1ЃЉжаЕФНсТлЪЧЗёЛЙГЩСЂЃПШєГЩСЂЃЌЧыгшвджЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЈбЁдёЭМ2ЃЌЭМ3жаЕФвЛжжЧщПігшвджЄУїЛђЫЕРэЃЉЃЛ
ЭтВПЪБЃЌЃЈ1ЃЉжаЕФНсТлЪЧЗёЛЙГЩСЂЃПШєГЩСЂЃЌЧыгшвджЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЈбЁдёЭМ2ЃЌЭМ3жаЕФвЛжжЧщПігшвджЄУїЛђЫЕРэЃЉЃЛ
ЃЈ3ЃЉШчЭМ4ЃЌЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЕФбгГЄЯпЩЯЪБЃЌСЌНг
ЕФбгГЄЯпЩЯЪБЃЌСЌНг![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓЫФБпаЮ
ЃЌЧѓЫФБпаЮ![]() ЕФУцЛ§.
ЕФУцЛ§.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉНсТлШдШЛГЩСЂЃЌРэгЩЃКТдЃЛЃЈ3ЃЉ
ЃЛЃЈ2ЃЉНсТлШдШЛГЩСЂЃЌРэгЩЃКТдЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
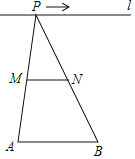
ЃЈ1ЃЉСЌНгACЃЌИљОнСтаЮЕФаджЪКЭЕШБпШ§НЧаЮЕФаджЪЕУГіЁїBAPЁеЁїCAEЃЌдйбгГЄ![]() НЛ
НЛ![]() гк
гк![]() ЃЌ ИљОнШЋЕШШ§НЧаЮЕФаджЪМДПЩЕУГіЃЛ
ЃЌ ИљОнШЋЕШШ§НЧаЮЕФаджЪМДПЩЕУГіЃЛ
ЃЈ2ЃЉНсТлШдШЛГЩСЂЃЎжЄУїЗНЗЈЭЌЃЈ1ЃЉЃЛ
ЃЈ3ЃЉИљОнЃЈ2ЃЉПЩжЊЁїBAPЁеЁїCAEЃЌИљОнЙДЙЩЖЈРэЗжБ№ЧѓГіAPКЭECЕФГЄЃЌ![]() МДПЩНтОіЮЪЬтЃЛ
МДПЩНтОіЮЪЬтЃЛ
ЃЈ1ЃЉШчЭМ1жаЃЌНсТлЃК![]() ЃЌ
ЃЌ![]() .
.
РэгЩЃКСЌНг![]() .
.
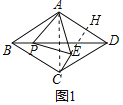
ЁпЫФБпаЮ![]() ЪЧСтаЮЃЌ
ЪЧСтаЮЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЖМЪЧЕШБпШ§НЧаЮЃЌ
ЖМЪЧЕШБпШ§НЧаЮЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЪЧЕШБпШ§НЧаЮЃЌ
ЪЧЕШБпШ§НЧаЮЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
бгГЄ![]() НЛ
НЛ![]() гк
гк![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() .
.
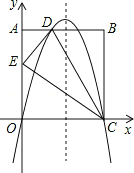
ЙЪД№АИЮЊ![]() ЃЌ
ЃЌ![]() .
.
ЃЈ2ЃЉНсТлШдШЛГЩСЂ.
РэгЩЃКбЁЭМ2ЃЌСЌНг![]() НЛ
НЛ![]() гк
гк![]() ЃЌЩш
ЃЌЩш![]() НЛ
НЛ![]() гк
гк![]() .
.

ЁпЫФБпаЮ![]() ЪЧСтаЮЃЌ
ЪЧСтаЮЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЖМЪЧЕШБпШ§НЧаЮЃЌ
ЖМЪЧЕШБпШ§НЧаЮЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЪЧЕШБпШ§НЧаЮЃЌ
ЪЧЕШБпШ§НЧаЮЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() .
.
 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() .
.
бЁЭМ3ЃЌСЌНг![]() НЛ
НЛ![]() гк
гк![]() ЃЌЩш
ЃЌЩш![]() НЛ
НЛ![]() гк
гк![]() .
.
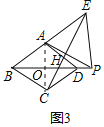
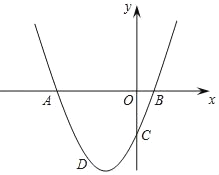
ЁпЫФБпаЮABCDЪЧСтаЮЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЖМЪЧЕШБпШ§НЧаЮЃЌ
ЖМЪЧЕШБпШ§НЧаЮЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЪЧЕШБпШ§НЧаЮЃЌ
ЪЧЕШБпШ§НЧаЮЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() .
.
 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() .
.
ЃЈ3ЃЉ![]() ЃЌ
ЃЌ
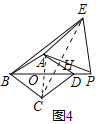
гЩЃЈ2ЃЉПЩжЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дкСтаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() гы
гы![]() ЪЧСтаЮЕФЖдНЧЯпЃЌ
ЪЧСтаЮЕФЖдНЧЯпЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
Ёр![]()
![]() .
.