题目内容
 根据多项式的乘法与因式分解的关系,可得x2-x-6=(x+2)(x-3),右边的两个一次两项式的系数有关系11×-32,左边上、下角两数积是原式左边二次项的系数,右边两数积是原式左边常数项,交叉相乘积之和是原式左边一次项的系数.这种分解二次三项式的方法叫“十字相乘法”.请同学们认真观察,分析理解后,解答下列问题.
根据多项式的乘法与因式分解的关系,可得x2-x-6=(x+2)(x-3),右边的两个一次两项式的系数有关系11×-32,左边上、下角两数积是原式左边二次项的系数,右边两数积是原式左边常数项,交叉相乘积之和是原式左边一次项的系数.这种分解二次三项式的方法叫“十字相乘法”.请同学们认真观察,分析理解后,解答下列问题.(1)填空:
①分解因数:6x2-x-2=
②解方程:3x2+x-2=0,左边分解因式得(
(2)解方程x2+
| 2 | x2-3 |
分析:(1)①利用十字相乘法,将6分解为2、3,将-2分解为1、-2,则6x2-x-2=(2x+1)(3x-2).
②利用十字相乘法,将二次项系数3分解为1、3,将常数项分解为1、-2,则3x2+x-2=(x+1)(3x-2).
②利用十字相乘法,将二次项系数3分解为1、3,将常数项分解为1、-2,则3x2+x-2=(x+1)(3x-2).
解答:解:(1)①、6x2-x-2=(2x+1)(3x-2).
②、3x2+x-2=0,
左边分解因式得(x+1)(3x-2)=0,
解得:x1=-1,x2=
;
(2)解方程两边都乘以(x2-3),
得x2(x2-3)+2=0,
化简得x4-3x2+2=0
设y=x2,则原方程为y2-3y+2=0,
解这个方程得y1=1,y2=2,
即x2=1或x2=2,
解这两个方程得x1=1,x2=-1,x3=
,x4=-
,
经检验,x1=1,x2=-1,x3=
,x4=-
均为原方程的根.
②、3x2+x-2=0,
左边分解因式得(x+1)(3x-2)=0,
解得:x1=-1,x2=
| 2 |
| 3 |
(2)解方程两边都乘以(x2-3),
得x2(x2-3)+2=0,
化简得x4-3x2+2=0
设y=x2,则原方程为y2-3y+2=0,
解这个方程得y1=1,y2=2,
即x2=1或x2=2,
解这两个方程得x1=1,x2=-1,x3=
| 2 |
| 2 |
经检验,x1=1,x2=-1,x3=
| 2 |
| 2 |
点评:本题考查了利用十字相乘法进行因式分解和解分式方程,十字相乘法在因式分解和解方程中有着广泛的应用,运用十字相乘法分解因式时,要注意观察,尝试,并体会它实质是二项式乘法的逆过程.在解分式方程时,当次数较高时,可应用换元法.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
| 由多项式的乘法法则知:若(x+a)(x+b)=x2+x+q,则p=a+b,q=a·b;反过来x2+x+q=(x+a)(x+b)要将多项式x2+x+q进行分解,关键是找到两个数a、b,使a+b=p,a·b=q,如对多项式x2-3x+2,有p=-3,q=2,a=-1,b=-2。此时(-1)+(-2)=-3,(-1)(-2)=2,所以x2-3x+2可分解为(x-1)(x-2)即x2-3x-2=(x-1)(x-2)。 (1)根据以上填写下表: | ||||||||||||||||||||||||||||||
当q是正数时,应分解成两个因数a、b_______________号,a、b的符号与__________相同; 当q是负数时,应分解成的两个因数a、b______________号,a、b中绝对值较大的因数的符号与_______相同。 (3)分解因式: x2-x-12=_____________;x2-7x+6=________________。 |
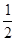 、
、 、
、
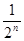 ,根据图示我们可以知道:
,根据图示我们可以知道: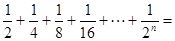 .
.
 .
. ;
; .
. 根据多项式的乘法与因式分解的关系,可得x2-x-6=(x+2)(x-3),右边的两个一次两项式的系数有关系11×-32,左边上、下角两数积是原式左边二次项的系数,右边两数积是原式左边常数项,交叉相乘积之和是原式左边一次项的系数.这种分解二次三项式的方法叫“十字相乘法”.请同学们认真观察,分析理解后,解答下列问题.
根据多项式的乘法与因式分解的关系,可得x2-x-6=(x+2)(x-3),右边的两个一次两项式的系数有关系11×-32,左边上、下角两数积是原式左边二次项的系数,右边两数积是原式左边常数项,交叉相乘积之和是原式左边一次项的系数.这种分解二次三项式的方法叫“十字相乘法”.请同学们认真观察,分析理解后,解答下列问题. .
. .
.