题目内容
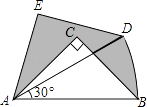
【题目】已知抛物线y=x2﹣2x+m﹣1与x轴只有一个交点,且与y轴交于A点,如图,设它的顶点为B.
(1)求m的值;
(2)过A作x轴的平行线,交抛物线于点C,求证:△ABC是等腰直角三角形;
(3)将此抛物线向下平移4个单位后,得到抛物线C′,且与x轴的左半轴交于E点,与y轴交于F点,如图.请在抛物线C′上求点P,使得△EFP是以EF为直角边的直角三角形.
【答案】
(1)
解:∵抛物线y=x2﹣2x+m﹣1与x轴只有一个交点,
∴△=(﹣2)2﹣4×1×(m﹣1)=0,
解得,m=2
(2)
解:由(1)知抛物线的解析式为y=x2﹣2x+1=(x﹣1)2,易得顶点B(1,0),
当x=0时,y=1,得A(0,1).
由1=x2﹣2x+1,解得,x=0(舍)或x=2,所以C点坐标为:(2,1).
过C作x轴的垂线,垂足为D,则CD=1,BD=xD﹣xB=1.
∴在Rt△CDB中,∠CBD=45°,BC= ![]() .
.
同理,在Rt△AOB中,AO=OB=1,于是∠ABO=45°,AB= ![]() .
.
∴∠ABC=180°﹣∠CBD﹣∠ABO=90°,AB=BC,
因此△ABC是等腰直角三角形
(3)
解:由题知,抛物线C′的解析式为y=x2﹣2x﹣3,
当x=0时,y=﹣3;
当y=0时,x=﹣1或x=3,
∴E(﹣1,0),F(0,﹣3),即OE=1,OF=3.
第一种情况:若以E点为直角顶点,设此时满足条件的点为P1(x1,y1),作P1M⊥x轴于M.
∵∠P1EM+∠OEF=∠EFO+∠OEF=90°,
∴∠P1EM=∠EFO,得Rt△EFO∽Rt△P1EM,
则 ![]() ,即EM=3P1M.
,即EM=3P1M.
∵EM=x1+1,P1M=y1,
∴x1+1=3y1①
由于P1(x1,y1)在抛物线C′上,
则有3(x12﹣2x1﹣3)=x1+1,
整理得,3x12﹣7x1﹣10=0,解得,
![]() ,或x2=﹣1(舍去)
,或x2=﹣1(舍去)
把 ![]() 代入①中可解得,
代入①中可解得,
y1= ![]() .
.
∴P1( ![]() ,
, ![]() ).
).
第二种情况:若以F点为直角顶点,设此时满足条件的点为P2(x2,y2),作P2N⊥y轴于N.
同第一种情况,易知Rt△EFO∽Rt△FP2N,
得 ![]() ,即P2N=3FN.
,即P2N=3FN.
∵P2N=x2,FN=3+y2,
∴x2=3(3+y2)②
由于P2(x2,y2)在抛物线C′上,
则有x2=3(3+x22﹣2x2﹣3),
整理得3x22﹣7x2=0,解得x2=0(舍)或 ![]() .
.
把 ![]() 代入②中可解得,
代入②中可解得,
![]() .
.
∴P2( ![]() ,
, ![]() ).
).
综上所述,满足条件的P点的坐标为:( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).


【解析】(1)根据抛物线与x轴只有一个交点可知△的值为0,由此得到一个关于m的一元一次方程,解此方程可得m的值;(2)根据抛物线的解析式求出顶点坐标,根据A点在y轴上求出A点坐标,再求C点坐标,根据三个点的坐标得出△ABC为等腰直角三角形;(3)根据抛物线解析式求出E、F的坐标,然后分别讨论以E为直角顶点和以F为直角顶点P的坐标.
【考点精析】认真审题,首先需要了解二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点),还要掌握二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小)的相关知识才是答题的关键.

 考前必练系列答案
考前必练系列答案