Question

【题目】如图，正方形ABCD边长为2，E为AB边的中点，点F是BC边上一个动点，把△BEF沿EF向形内部折叠，点B的对应点为B′，当B′D的长最小时，BF长为（ ）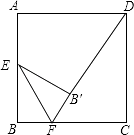
A.
B. ﹣1
C.
D.

Answer 1

【答案】D
【解析】解；如图，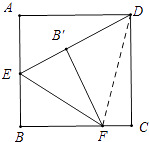
当E．B′、D共线时，DB′最小，此时DB′=ED﹣EB′=ED﹣EB．
在RT△AED中，∵AD=2，AE=1，
∴DE= = ，
∴DB′=DE=EB= ﹣1．
设BF=x，
∵DF2=DB′2+B′F2=CD2+CF2 ，
∴x2+（ ﹣1）2=22+（2﹣x）2 ，
∴x= ．
故选D．
【考点精析】认真审题，首先需要了解正方形的性质(正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)，还要掌握翻折变换（折叠问题）(折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等)的相关知识才是答题的关键．