题目内容
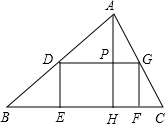
如图，P是矩形ABCD内的任意一点，连接PA、PB、PC、PD，得到△PAB、△PBC、△PCD、△PDA，设它们的面积分别是S1、S2、S3、S4，给出如下结论：
①S1+S2=S3+S4 ② S2+S4= S1+ S3 ③若S3=2 S1，则S4=2 S2 ④若S1= S2，则P点在矩形的对角线上其中正确的结论的序号是_________________（把所有正确结论的序号都填在横线上）.
解析：过点P分别向AD、BC作垂线段，两个三角形的面积之和
等于矩形面积的一半，同理，过点P分别向AB、CD作垂线段，两个三角形的面积之和
等于矩形面积的一半. =,又因为
，则
=
,所以④一定成立
答案：②④．
点评：本题利用三角形的面积计算，能够得出②成立，要判断④成立，在这里充分利用所给条件，对等式进行变形.不要因为选出②，就认为找到答案了，对每个结论都要分析，当然感觉不一定对的，可以举反例即可.对于 ④这一选项容易漏选.
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
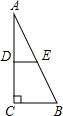如图，在一张△ABC纸片中，∠C=90°，∠B=60°，DE是中位线，现把纸片沿中位线DE剪开，计划拼出以下四个图形：①邻边不等的矩形；②等腰梯形；③有两个角为锐角的菱形；④正方形．那么以上图形一定能被拼成的个数为（ ）
