题目内容

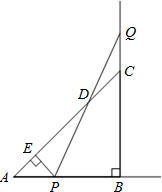如图，△ABC中，∠B=90°，AB=BC=2，点P，Q分别从A，C两点同时出发，以相同速度作直线运动，已知点P沿射线AB运动（与A、B不重合），点Q沿边BC的延长线运动．PQ与直线AC相交于点D．
（1）设AP的长为x，△PBQ的面积为S，求出S与x的函数关系式．并指出自变量的取值范围．
（2）△PBQ的面积与△ABC的面积能相等吗？若能相等，求出x的值；若不能相等，说明理由．

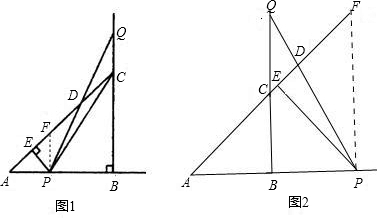解：（1）①当点P在线段AB上时（如图1），此时0＜x≤2．
∵AP=CQ=x，
∴BQ=2+x，PB=2-x．
∴S_△PBQ= $\text{[math]}$ BQ•PB= $\text{[math]}$ （2+x）（2-x）．
即S= $\text{[math]}$ （4-x²）（0＜x＜2）；
②当点P在AB延长线上时（如图2），此时x＞2．
∵AP=CQ=x，
∴BQ=2+x，PB=x-2．
∴S_△PBQ= $\text{[math]}$ BQ•PB= $\text{[math]}$ （2+x）（x-2）．
即S= $\text{[math]}$ （x²-4）（x＞2）；

（2）S_△ABC= $\text{[math]}$ ×2×2=2．
①令 $\text{[math]}$ （4-x²）=2，即x²=0，x=0不符合题意；
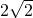②令 $\text{[math]}$ （x²-4）=2，即x²=8，解得x= $\text{[math]}$ （负值舍去）．
故当AP的长为2 $\text{[math]}$ 时，△PBQ的面积与△ABC的面积相等．
分析：（1）本题要分两种情况进行讨论：①当P在线段AB上；②当P在AB延长线上．△PBQ都是以BQ为底，PB为高，可据此得出S、x的函数关系式；
（2）先计算出△ABC的面积，然后将其值代入（1）中得出的函数式中，如果方程有解且符合题意，则能相等，否则就不能相等．
点评：本题结合三角形的相关知识考查了二次函数的应用，主要考查了学生分类讨论、数形结合的数学思想方法．