题目内容
 如图,P是边长为4的正方形ABCD的边AD上的一点,且PE⊥AC,PF⊥BD,则PE+PF=
如图,P是边长为4的正方形ABCD的边AD上的一点,且PE⊥AC,PF⊥BD,则PE+PF=分析:根据条件可以得到四边形PEOF是矩形,因而PF=OE,同时易证△APE是等腰直角三角形,因而AE=PE,则PE+PF=OA.根据勾股定理即可求解.
解答:解:∵四边形ABCD是正方形,边长为4,
∴AD=CD=4 AC⊥BD∠DAO=45°;
∴AC2=AD2+CD2=42+42=32,则AC=4
,
∵PE⊥AC,PF⊥BD,
∴∠PEC=∠PFB=90°;
又∵AC⊥BD,
∴四边形EPFO是矩形;
∴PF=OE,
又∵∠DAO=∠APE=45°,
∴AE=PE;
∵AE+OE=OA=
AC=
×4
=2
,
∴PE+PF=2
.
故答案为2
.
∴AD=CD=4 AC⊥BD∠DAO=45°;
∴AC2=AD2+CD2=42+42=32,则AC=4
| 2 |
∵PE⊥AC,PF⊥BD,
∴∠PEC=∠PFB=90°;
又∵AC⊥BD,
∴四边形EPFO是矩形;
∴PF=OE,
又∵∠DAO=∠APE=45°,
∴AE=PE;
∵AE+OE=OA=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∴PE+PF=2
| 2 |
故答案为2
| 2 |
点评:此题较简单,根据正方形的性质及勾股定理解答即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )
14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )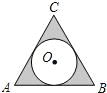 如图,⊙O是边长为2的等边三角形ABC的内切圆,则图中阴影部分的面积为
如图,⊙O是边长为2的等边三角形ABC的内切圆,则图中阴影部分的面积为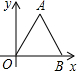 如图,△AOB是边长为5的等边三角形,则A,B两点的坐标分别是A
如图,△AOB是边长为5的等边三角形,则A,B两点的坐标分别是A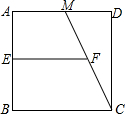 如图,M是边长为2cm的正方形ABCD的边AD的中点,E、F分别是AB、CM的中点.则EF=
如图,M是边长为2cm的正方形ABCD的边AD的中点,E、F分别是AB、CM的中点.则EF= 如图,△ABC是边长为6的等边三角形,AD=2,AE∥BC,直线BD交AE于点E,则BE的长为( )
如图,△ABC是边长为6的等边三角形,AD=2,AE∥BC,直线BD交AE于点E,则BE的长为( )