题目内容
如图,D是边长为4cm的等边△ABC的边AB上的一点,作DQ⊥AB交边BC于点Q,RQ⊥BC交边AC于点R,RP⊥AC交边AB于点E,交QD的延长线于点P.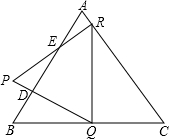
(1)请说明△PQR是等边三角形的理由;
(2)若BD=1.3cm,则AE=
(3)如图,当点E恰好与点D重合时,求出BD的长度.
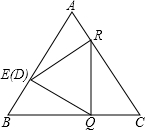
分析:△PQR是等边△的理由就是可以求出∠DQR和∠PRQ都是60°,灵活运用Rt△中30°所对的边是斜边的一半的知识.
解答: 解:(1)根据题意,△ABC为等边三角形,
解:(1)根据题意,△ABC为等边三角形,
∴∠B=60°.
又∵DQ⊥AB,
∴∠B+∠BQD=∠BQD+∠PQR=90°,
∴∠PQR=60°.
同理,得
∠PRQ=60°
∴△PQR是等边三角形;
(2)∠DQB=30°,BD=1.3cm,
∴BQ=2.6cm,
CQ=4-2.6=1.4CM,
∠QRC=30°,
∴CR=2.8cm,
AR=4-2.8=1.2cm,
∠AER=30°,
AE=2AR=2.4cm;
(3)易证△BDQ≌△RQC≌△ADR,
∴DB=AR,
∵RQ⊥BC,∠A=60°,
∴2AR=AD,
∴3DB=AB,
∴DB=
×4=
(cm).
 解:(1)根据题意,△ABC为等边三角形,
解:(1)根据题意,△ABC为等边三角形,∴∠B=60°.
又∵DQ⊥AB,
∴∠B+∠BQD=∠BQD+∠PQR=90°,
∴∠PQR=60°.
同理,得
∠PRQ=60°
∴△PQR是等边三角形;
(2)∠DQB=30°,BD=1.3cm,
∴BQ=2.6cm,
CQ=4-2.6=1.4CM,
∠QRC=30°,
∴CR=2.8cm,
AR=4-2.8=1.2cm,
∠AER=30°,
AE=2AR=2.4cm;

(3)易证△BDQ≌△RQC≌△ADR,
∴DB=AR,
∵RQ⊥BC,∠A=60°,
∴2AR=AD,
∴3DB=AB,
∴DB=
| 1 |
| 3 |
| 4 |
| 3 |
点评:本题主要考查了等边三角形的性质和判定三角形全等的方法.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )
14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )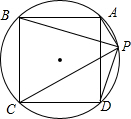 如图,⊙O是边长为1的正方形ABCD的外接圆,P为弧AD上的不同于A、D的任意一点,则PA2+PB2+PC2+PD2的值为( )
如图,⊙O是边长为1的正方形ABCD的外接圆,P为弧AD上的不同于A、D的任意一点,则PA2+PB2+PC2+PD2的值为( )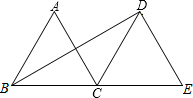 如图,△ABC是边长为
如图,△ABC是边长为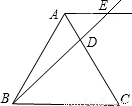
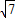
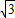
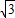
 如图,⊙O是边长为1的正方形ABCD的外接圆,P为弧AD上的不同于A、D的任意一点,则PA2+PB2+PC2+PD2的值为( )
如图,⊙O是边长为1的正方形ABCD的外接圆,P为弧AD上的不同于A、D的任意一点,则PA2+PB2+PC2+PD2的值为( )