题目内容
 如图,三角形ABC的面积为1,BD:DC=2:1,E为AC的中点,AD与BE相交于P,那么四边形PDCE的面积为________.
如图,三角形ABC的面积为1,BD:DC=2:1,E为AC的中点,AD与BE相交于P,那么四边形PDCE的面积为________.
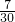
分析:连接CP.设△CPE的面积是x,△CDP的面积是y.根据BD:DC=2:1,E为AC的中点,得△BDP的面积是2y,△APE的面积是x,进而得到△ABP的面积是4x.再根据△ABE的面积是△BCE的面积相等,得4x+x=2y+x+y,解得y=
 x,再根据△ABC的面积是1即可求得x、y的值,从而求解.
x,再根据△ABC的面积是1即可求得x、y的值,从而求解.解答:
 解:连接CP,
解:连接CP,设△CPE的面积是x,△CDP的面积是y.
∵BD:DC=2:1,E为AC的中点,
∴△BDP的面积是2y,△APE的面积是x,
∵BD:DC=2:1,CE:AC=2:1,
∴△ABP的面积是4x.
∴4x+x=2y+x+y,
解得y=
 x.
x.又∵4x+x=
 ,
,x=
 .
.则四边形PDCE的面积为x+y=
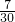 .
.故答案为:
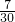 .
.点评:此题能够根据三角形的面积公式求得三角形的面积之间的关系.等高的两个三角形的面积比等于它们的底的比;等底的两个三角形的面积比等于它们的高的比.

练习册系列答案
相关题目
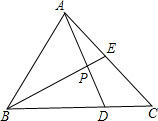 如图,三角形ABC的面积为1,BD:DC=2:1,E为AC的中点,AD与BE相交于P,那么四边形PDCE的面积为
如图,三角形ABC的面积为1,BD:DC=2:1,E为AC的中点,AD与BE相交于P,那么四边形PDCE的面积为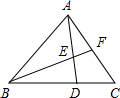 如图,三角形ABC的面积是30平方厘米,AE=ED、BD=
如图,三角形ABC的面积是30平方厘米,AE=ED、BD= (2012•潍坊)如图,三角形ABC的两个顶点B、C在圆上,顶点A在圆外,AB、AC分别交圆于E、D两点,连接EC、BD.
(2012•潍坊)如图,三角形ABC的两个顶点B、C在圆上,顶点A在圆外,AB、AC分别交圆于E、D两点,连接EC、BD.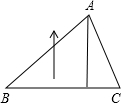 如图,三角形ABC的底边BC长3厘米,BC边上的高是2厘米,将三角形以每秒3厘米的速度沿高的方向向上移动2秒,这时,三角形扫过的面积是多少平方厘米( )
如图,三角形ABC的底边BC长3厘米,BC边上的高是2厘米,将三角形以每秒3厘米的速度沿高的方向向上移动2秒,这时,三角形扫过的面积是多少平方厘米( )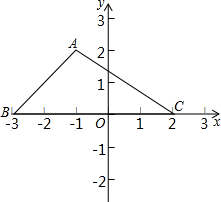 如图,三角形ABC的顶点坐标分别是A(-1,2),B(-3,0),C(2,0),求△ABC的面积.
如图,三角形ABC的顶点坐标分别是A(-1,2),B(-3,0),C(2,0),求△ABC的面积.