题目内容
双曲线y=
上一点P,过P作x轴,y轴的垂线,垂足分别为A、B,矩形OAPB的面积为2,则双曲线与直线在y=kx-4交点在第一象限内的点的坐标为
| k |
| x |
(1+
,2
-2)
| 3 |
| 3 |
(1+
,2
-2)
.| 3 |
| 3 |
分析:根据反比例函数与一次函数的交点在第一象限,可以确定反比例系数k>0,然后根据反比例函数的系数k的集合意义求得k的值,得到两个函数的解析式,然后解方程组即可求得交点坐标.
解答:解:∵双曲线与直线在y=kx-4交点在第一象限内的点,
∴k>0,
又∵矩形OAPB的面积为2,
∴k=2,
则反比例函数与直线的解析式是:y=
和y=2x-4,
解方程组:
,
解得:x=1±
,当交点在第一象限时,x=1+
,
代入直线的解析式得:y=2(1+
)-4=2
-2,
则在第一象限的交点坐标是:(1+
,2
-2).
故答案是:(1+
,2
-2).
∴k>0,
又∵矩形OAPB的面积为2,
∴k=2,
则反比例函数与直线的解析式是:y=
| 2 |
| x |
解方程组:
|
解得:x=1±
| 3 |
| 3 |
代入直线的解析式得:y=2(1+
| 3 |
| 3 |
则在第一象限的交点坐标是:(1+
| 3 |
| 3 |
故答案是:(1+
| 3 |
| 3 |
点评:本题综合考查反比例函数与方程组的相关知识点.先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,正确理解反比例函数的比例系数大于0是关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
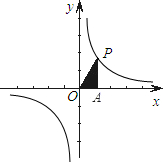 如图,P是双曲线y=
如图,P是双曲线y=| k |
| x |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、-2 |
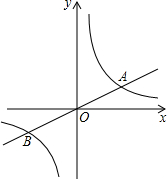 如图,直线
如图,直线 (2011•成华区二模)如图,已知点A是双曲线
(2011•成华区二模)如图,已知点A是双曲线