题目内容
(1)|2-tan60°|-(π-3.14)0+(-
)-2+
(2)已知正比例函数y=2x的图象与反比例函数y=
的图象有一个交点的纵坐标是2.
①求反比例函数解析式;
②当-3≤x≤-1时,求反比例函数y的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
(2)已知正比例函数y=2x的图象与反比例函数y=
| k |
| x |
①求反比例函数解析式;
②当-3≤x≤-1时,求反比例函数y的取值范围.
分析:(1)首先计算特殊角的三角函数值,计算乘方,进行开方,然后合并同类二次根式即可求解;
(2)①把y=2代入y=2x,求得函数的交点坐标,然后把交点坐标代入反比例函数的解析式即可求得反比例函数;
②求出当x=-3和x=-1时,反比例函数的函数值,即可确定.
(2)①把y=2代入y=2x,求得函数的交点坐标,然后把交点坐标代入反比例函数的解析式即可求得反比例函数;
②求出当x=-3和x=-1时,反比例函数的函数值,即可确定.
解答:解:(1)原式=|2-
|-1+4+
=2-
-1+4+
=5;
(2)①把y=2代入y=2x得:x=1,则交点坐标是:(1,2),
代入y=
得:4=
,解得:k=2,
则函数的解析式是:y=
;
②当x=-3时,y=-
;
当x=-1时,y=-2,
则反比例函数y的取值范围是:-2≤y≤-
.
| 3 |
| 3 |
=2-
| 3 |
| 3 |
=5;
(2)①把y=2代入y=2x得:x=1,则交点坐标是:(1,2),
代入y=
| k |
| x |
| k |
| 2 |
则函数的解析式是:y=
| 2 |
| x |
②当x=-3时,y=-
| 2 |
| 3 |
当x=-1时,y=-2,
则反比例函数y的取值范围是:-2≤y≤-
| 2 |
| 3 |
点评:本题考查了0指数幂以及负指数幂,反比例函数与一次函数的交点,正确求得函数的解析式是关键.

练习册系列答案
相关题目
 如图所示,△ABC内接于⊙O,AB是直径,D是
如图所示,△ABC内接于⊙O,AB是直径,D是
 sin60°•tan45°;
sin60°•tan45°;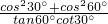 +tan60°;
+tan60°;