题目内容
如图,在平面直角坐标系,A,B两点的坐标分别为(0,-2),(0,8),以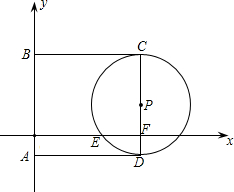 AB为一边作正方形ABCD,再以CD为直径的半圆P.设x轴交半圆P于点E,交边CD于点F.
AB为一边作正方形ABCD,再以CD为直径的半圆P.设x轴交半圆P于点E,交边CD于点F.(1)求线段EF的长;
(2)连接BE,试判断直线B与⊙P的位置关系,并说明你的理由;
(3)直线BE上是否存在着点Q,使得以Q为圆心、r为半径的圆,既与y轴相切又与⊙P外切?若存在,试求r的值;若不存在,请说明理由.
分析:(1)线段EF的长,在△EFP中,根据勾股定理求出;
(2)要想证BE是⊙O的切线,只要连接PE,求证∠PEB=90°即可;
(3)求r的值,因为⊙Q与⊙P外切有PQ=r+5,Q与y轴相切有QM=r,则QN=MN-QM=10-r,则通过证明△BMQ∽△BOE可求NP=5-
,在Rt△QNP中由勾股定理得出QN2+NP2=PQ2,列出关于r的方程,求出r的值.
(2)要想证BE是⊙O的切线,只要连接PE,求证∠PEB=90°即可;
(3)求r的值,因为⊙Q与⊙P外切有PQ=r+5,Q与y轴相切有QM=r,则QN=MN-QM=10-r,则通过证明△BMQ∽△BOE可求NP=5-
| 4r |
| 3 |
解答: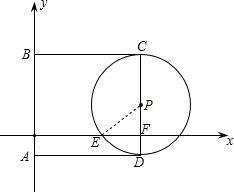 解:(1)连接PE,EF=
解:(1)连接PE,EF=
=
=4(3分)
(2)(解法一)
∵
=
=2,
=
=2,
∴Rt△BOE∽Rt△EFP.
∴∠OBE=∠FEP.
∴∠OBE+∠OEB=90°?∠FEP+∠OEB=90°?∠BEP=90°.
∴直线B与⊙P相切.(3分)
(解法二)连接PB,
在Rt△PCB中,PB2=PC2+BC2=52+102=125,
在Rt△BOE中,BE2=BO2+OE2=82+62=100,
在△PEB中,BE2+PE2=100+25=PB2
∴∠PEB=90°.(3分)
∴直线B与⊙P相切.(1分)
(3)连接PQ,
∵⊙Q与⊙P外切,
∴PQ=r+5.(1分)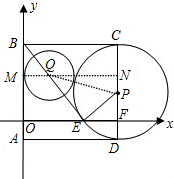
过Q作QM⊥y轴于M,交CD于N,
∵⊙Q与y轴相切,
∴QM=r.
∴QN=MN-QM=10-r.(1分)
∵MQ∥OE,
∴△BMQ∽△BOE.
∴
=
.
∴BM=
=
.
∴NP=NF-PF=MO-PF=BO-BM-PF=5-
.(2分)
(另解:直线DE所对应的函数关系式为y=-
x+8,设Q(r,h),代入得h=-
r+8,即NF=-
+8,从而NP=5-
)
∵在Rt△QNP中,QN2+NP2=PQ2∴(10-r)2+(5-
)2=(5+r)2
∴16r2-390r+900=0.(1分)
解得:r=
=
.(1分)
 解:(1)连接PE,EF=
解:(1)连接PE,EF=| PE2-PF2 |
| 52-32 |
(2)(解法一)
∵
| BO |
| EF |
| 8 |
| 4 |
| EO |
| PF |
| 10-4 |
| 3 |
∴Rt△BOE∽Rt△EFP.
∴∠OBE=∠FEP.
∴∠OBE+∠OEB=90°?∠FEP+∠OEB=90°?∠BEP=90°.
∴直线B与⊙P相切.(3分)
(解法二)连接PB,
在Rt△PCB中,PB2=PC2+BC2=52+102=125,
在Rt△BOE中,BE2=BO2+OE2=82+62=100,
在△PEB中,BE2+PE2=100+25=PB2
∴∠PEB=90°.(3分)
∴直线B与⊙P相切.(1分)
(3)连接PQ,
∵⊙Q与⊙P外切,
∴PQ=r+5.(1分)

过Q作QM⊥y轴于M,交CD于N,
∵⊙Q与y轴相切,
∴QM=r.
∴QN=MN-QM=10-r.(1分)
∵MQ∥OE,
∴△BMQ∽△BOE.
∴
| BM |
| BO |
| MQ |
| OE |
∴BM=
| 8×r |
| 6 |
| 4r |
| 3 |
∴NP=NF-PF=MO-PF=BO-BM-PF=5-
| 4r |
| 3 |
(另解:直线DE所对应的函数关系式为y=-
| 4 |
| 3 |
| 4 |
| 3 |
| 4r |
| 3 |
| 4r |
| 3 |
∵在Rt△QNP中,QN2+NP2=PQ2∴(10-r)2+(5-
| 4r |
| 3 |
∴16r2-390r+900=0.(1分)
解得:r=
195±
| ||
| 16 |
195±15
| ||
| 16 |
点评:本题难度较大,综合性较强,考查了正方形,直角三角形的性质,直线与圆,圆与圆的关系,切线的判断,相似三角形的性质及函数知识.

练习册系列答案
相关题目
 如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.
如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD. (2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是
(2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是 如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(4,0),D点坐标为(0,3),则AC长为
如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(4,0),D点坐标为(0,3),则AC长为 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数 ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.