题目内容
把一矩形纸片对折,若对折后所得的矩形与原矩形相似,则对折后的矩形与原矩形的相似比为
.
| ||
| 2 |
| ||
| 2 |
分析:设原矩形的长为2a,宽为b,表示出对折后的矩形的宽为a,然后根据相似多边形对应边成比例列出比例式求出
,即可得解.
| a |
| b |
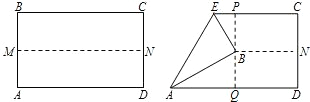
解答: 解:如图,设原矩形的长为2a,宽为b,
解:如图,设原矩形的长为2a,宽为b,
则对折后的矩形的长为b,宽为a,
∵对折后所得的矩形与原矩形相似,
∴
=
,
∴
=
,
即对折后的矩形与原矩形的相似比为
.
故答案为:
.
 解:如图,设原矩形的长为2a,宽为b,
解:如图,设原矩形的长为2a,宽为b,则对折后的矩形的长为b,宽为a,
∵对折后所得的矩形与原矩形相似,
∴
| a |
| b |
| b |
| 2a |
∴
| a |
| b |
| ||
| 2 |
即对折后的矩形与原矩形的相似比为
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了相似多边形对应边成比例的性质,是基础题,作出图形更形象直观.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
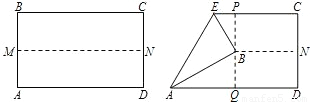
 24、小明打算用如图的矩形纸片ABCD折出一个等边三角形.他的操作步骤是:
24、小明打算用如图的矩形纸片ABCD折出一个等边三角形.他的操作步骤是: