题目内容
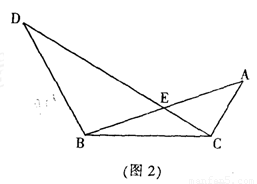
如图，C在AB的延长线上，CE⊥AF于E，交FB于D，若∠F=40°，∠C=20°，求∠FBA的度数．
解：在直角△EFD中，∠EDF=90°-∠F=90°-40=50°，
∴∠BDC=∠EDF=50°，
∴∠FBA=∠C+∠BDC=50°+20°=70°．
分析：在直角△EFD中，根据直角三角形的两锐角互余即可求得∠EDF，根据对顶角相等即可求得∠BDC，然后根据三角形的外角的性质即可求解．
点评：本题考查了直角三角形的性质，以及三角形的外角的性质，正确理解性质是关键．
∴∠BDC=∠EDF=50°，
∴∠FBA=∠C+∠BDC=50°+20°=70°．
分析：在直角△EFD中，根据直角三角形的两锐角互余即可求得∠EDF，根据对顶角相等即可求得∠BDC，然后根据三角形的外角的性质即可求解．
点评：本题考查了直角三角形的性质，以及三角形的外角的性质，正确理解性质是关键．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
如图点D在△ABC的AB边上，AD=BD=CD=1，延长BC至E，BC=CE，连接AE，则AE=
