题目内容
如图,对称轴为直线x= 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线的解析式及抛物线与x轴的另一交点C的坐标;
(2)D为坐标平面上一点,且以A、B、C、D为顶点的四边形是平行四边形,写出点D的坐标;
(3)如图2,点E(x,y)是抛物线上位于第四象限的一点,四边形OEAF是以OA为对角线的平行四边形.
①当□OEAF的面积为24时,请判断□OEAF是矩形吗?是菱形吗?
②是否存在点E,使□OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.


解:(1)由抛物线的对称轴是 ,可设解析式为
,可设解析式为 .
.
把A、B两点坐标代入上式,得

解之,得
故抛物线解析式为 (或
(或 .
.
当 时,
时, , ∴C(1,0)
, ∴C(1,0)
(2)
(3)①根据题意,当S = 24时,即 .
.
化简,得 解之,得
解之,得
故所求的点E有两个,分别为 .
.
因为OE不垂直于AE,所以□OEAF不可能是矩形.
因为点 满足OE = AE,所以□OEAF是菱形;
满足OE = AE,所以□OEAF是菱形;
因为点 不满足OE = AE,所以□OEAF不是菱形
不满足OE = AE,所以□OEAF不是菱形
当OA⊥EF,且OA = EF时,□OEAF是正方形,此时点E的坐标只能是(3,-3).而坐标为(3,-3)的点不在抛物线上,


练习册系列答案
相关题目
 B.
B. C.
C. D.
D.

 ,求图中阴影部分的面积.
,求图中阴影部分的面积. 
 , 则BC的长是( )
, 则BC的长是( ) D.4
D.4
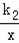 (k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,
(k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,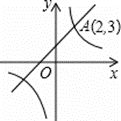
 的解是( )
的解是( ) 