题目内容



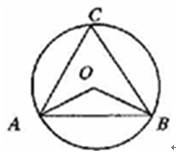
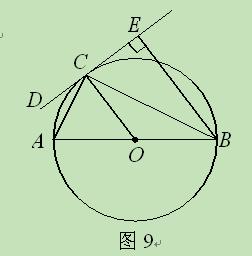
连接OB、OC,过O点作OD⊥BC于点D,由 可求出∠BOC=120°,再由垂径定理可知BD=
可求出∠BOC=120°,再由垂径定理可知BD= BC,根据锐角三角函数的定义可求出BD的长,进而可得出BC的长.
BC,根据锐角三角函数的定义可求出BD的长,进而可得出BC的长.
解:连接OB、OC,过O点作OD⊥BC于点D,

∵ =120°,
=120°,
∴∠BOC=120°,
∵OD⊥BC,
∴BD= BC,∠BOD=
BC,∠BOD= ∠BOC=
∠BOC= ×120°=60°,
×120°=60°,
在Rt△OBD中,BD=OB?sin∠BOD=5×
∴BC=2BD=2× =5
=5 .
.
故答案为:5 .
.
 可求出∠BOC=120°,再由垂径定理可知BD=
可求出∠BOC=120°,再由垂径定理可知BD= BC,根据锐角三角函数的定义可求出BD的长,进而可得出BC的长.
BC,根据锐角三角函数的定义可求出BD的长,进而可得出BC的长.解:连接OB、OC,过O点作OD⊥BC于点D,

∵
 =120°,
=120°,∴∠BOC=120°,
∵OD⊥BC,
∴BD=
 BC,∠BOD=
BC,∠BOD= ∠BOC=
∠BOC= ×120°=60°,
×120°=60°,在Rt△OBD中,BD=OB?sin∠BOD=5×

∴BC=2BD=2×
 =5
=5 .
.故答案为:5
 .
.
练习册系列答案
相关题目
 2,求BC的值.
2,求BC的值.
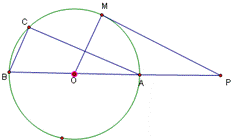
 上任一点(点P不与点A、B重合),连AP、BP,过点C作CM∥BP交的延长线于
上任一点(点P不与点A、B重合),连AP、BP,过点C作CM∥BP交的延长线于 点M.
点M.
 与⊙
与⊙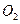 相交于
相交于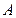 、
、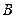 两点,点
两点,点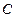 为⊙
为⊙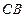 与⊙
与⊙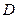 。
。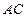 是⊙
是⊙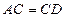 ;
;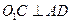 ;
;