题目内容
(本小题满分9分)已知⊙ 与⊙
与⊙ 相交于
相交于 、
、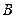 两点,点
两点,点 在⊙
在⊙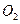 上,
上,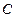 为⊙
为⊙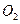 上一点(不与
上一点(不与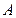 ,
,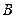 ,
, 重合),直线
重合),直线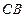 与⊙
与⊙ 交于另一点
交于另一点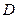 。
。
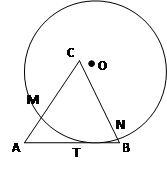
(1)如图(8),若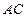 是⊙
是⊙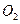 的直径,求证:
的直径,求证: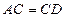 ;
;
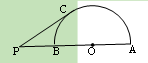
(2)如图(9),若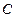 是⊙
是⊙ 外一点,求证:
外一点,求证: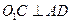 ;
;
(3)如图(10),若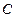 是⊙
是⊙ 内一点,判断(2)中的结论是否成立。
内一点,判断(2)中的结论是否成立。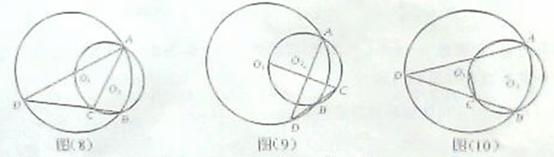
 与⊙
与⊙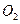 相交于
相交于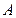 、
、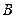 两点,点
两点,点 在⊙
在⊙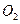 上,
上,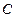 为⊙
为⊙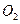 上一点(不与
上一点(不与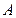 ,
,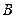 ,
, 重合),直线
重合),直线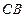 与⊙
与⊙ 交于另一点
交于另一点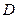 。
。(1)如图(8),若
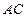 是⊙
是⊙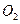 的直径,求证:
的直径,求证: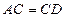 ;
;(2)如图(9),若
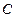 是⊙
是⊙ 外一点,求证:
外一点,求证: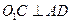 ;
;(3)如图(10),若
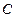 是⊙
是⊙ 内一点,判断(2)中的结论是否成立。
内一点,判断(2)中的结论是否成立。
证明:(1)如图(一),连接 ,
,
∵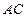 为⊙
为⊙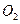 的直径 ∴
的直径 ∴
∴ 为⊙
为⊙ 的直径 ∴
的直径 ∴ 在
在 上
上
又 ,
, 为
为 的中点
的中点
∴△ 是以
是以 为底边的等腰三角形
为底边的等腰三角形
∴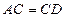 ····················································································· (3分)
····················································································· (3分)
(2)如图(二),连接 ,并延长
,并延长 交⊙
交⊙ 与点
与点 ,连
,连
∵四边形 内接于⊙
内接于⊙ ∴
∴
又∵ ∴
∴
∴
又 为⊙
为⊙ 的直径 ∴
的直径 ∴
∴ ···················································································· (3分)
···················································································· (3分)
(3)如图(三),连接 ,并延长
,并延长 交⊙
交⊙ 与点
与点 ,连
,连
∵ 又
又
∴
∴ 又
又
∴ ···················································································· (3分)
···················································································· (3分)
 ,
,
∵
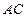 为⊙
为⊙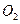 的直径 ∴
的直径 ∴
∴
 为⊙
为⊙ 的直径 ∴
的直径 ∴ 在
在 上
上又
 ,
, 为
为 的中点
的中点∴△
 是以
是以 为底边的等腰三角形
为底边的等腰三角形∴
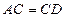 ····················································································· (3分)
····················································································· (3分)(2)如图(二),连接
 ,并延长
,并延长 交⊙
交⊙ 与点
与点 ,连
,连
∵四边形
 内接于⊙
内接于⊙ ∴
∴
又∵
 ∴
∴
∴

又
 为⊙
为⊙ 的直径 ∴
的直径 ∴
∴
 ···················································································· (3分)
···················································································· (3分)(3)如图(三),连接
 ,并延长
,并延长 交⊙
交⊙ 与点
与点 ,连
,连
∵
 又
又
∴

∴
 又
又
∴
 ···················································································· (3分)
···················································································· (3分)略

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 的度数( )
的度数( )