题目内容
某校要把一块形状是直角三角形的废地开发为生物园．如图所示，∠ACB=90°，AC=80m，BC=60m．若线段CD为一条水渠，且D在边AB上，当水渠长度最短时，在图中画出线段CD，并求出水渠CD的长度．考点：作图—应用与设计作图,垂线段最短
专题：应用题
分析：过点C作CD⊥AB于点D，则线段CD即为所求，再根据勾股定理求出AB的长，根据三角形的面积公式即可得出结论．
解答：
解：过点C作CD⊥AB于点D，
∵∠ACB=90°，AC=80m，BC=60m，
∴AB=
=
=100m，
∴CD=
=
=48（m）．
答：水渠CD的长度为48米．
解：过点C作CD⊥AB于点D，∵∠ACB=90°，AC=80m，BC=60m，
∴AB=
| AC2+BC2 |
| 802+602 |
∴CD=
| AC•BC |
| AB |
| 80×60 |
| 100 |
答：水渠CD的长度为48米．
点评：本题考查的是作图-应用与设计作图，熟知“垂线段最短”是解答此题的关键．
练习册系列答案
相关题目
如图，若使△ABC≌△ADC，则需添加的条件是（ ）| A、AB=AD，∠B=∠D |
| B、AB=AD，∠ACB=∠ACD |
| C、BC=DC，∠BAC=∠DAC |
| D、AB=AD，∠BAC=∠DAC |
在
，
，
，
，
中，分式的个数是（ ）
| 8 |
| 5 |
| 3m |
| n |
| x+y |
| 3 |
| 1 |
| x |
| 3 |
| a+b |
| A、1 | B、2 | C、3 | D、4 |
如图，正方形ABCD的边长为2，动点P从点D出发，沿折线D→C→B作匀速运动，则△APD的面积S与点P运动的路程x之间的函数图象大致是（ ）
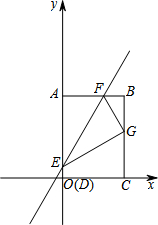如图，四边形ABCD为矩形，点D与坐标原点重合，点C在x轴上，点A在y轴上，点B的坐标是（8，12），矩形ABCD沿直线EF折叠，点A落在BC边上的G处，点E，F分别在AD，AB上，且F点的坐标是（5，12）．