题目内容
12.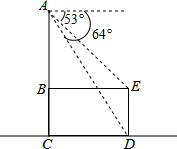 如图是放在水平地面上的一把椅子的侧面图,椅子高为AC,椅面宽为BE,椅脚高为ED,且AC⊥BE,AC⊥CD,AC∥ED.从点A测得点D、E的俯角分别为64°和53°.已知ED=35cm,求椅子高AC约为多少?
如图是放在水平地面上的一把椅子的侧面图,椅子高为AC,椅面宽为BE,椅脚高为ED,且AC⊥BE,AC⊥CD,AC∥ED.从点A测得点D、E的俯角分别为64°和53°.已知ED=35cm,求椅子高AC约为多少?(参考数据:tan53°≈$\frac{4}{3}$,sin53°≈$\frac{4}{5}$,tan64°≈2,sin64°≈$\frac{9}{10}$)
分析 根据正切函数的定义,可得方程①②,根据代入消元法,可得答案.
解答 解:在Rt△ACD中,tan∠ADC=tan64°=$\frac{AC}{CD}$=2,
CD=$\frac{AC}{2}$ ①.
在Rt△ABE中tan∠ABE=tan53°=$\frac{AB}{BE}$=$\frac{4}{3}$,
BE=$\frac{3}{4}$AB ②.
BE=CD,得$\frac{AC}{2}$=$\frac{AB+DE}{2}$=$\frac{AB+35}{2}$=$\frac{3}{4}$AB,
解得AB=70cm,
AC=AB+BC=AB+DE=70+35=105cm.
点评 本题考查了解直角三角形的应用,利用正切函数得出方程①②是解题关键.

练习册系列答案
相关题目
20.下列运算正确的是( )
| A. | a-2=-a2 | B. | a+a2=a3 | C. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | D. | (a2)3=a6 |
17.下列是某校教学活动小组学生的年龄情况:13,15,15,16,13,15,14,15(单位:岁).这组数据的中位数和极差分别是( )
| A. | 15,3 | B. | 14,15 | C. | 16,16 | D. | 14,3 |
1.为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2015年4月份用电量的调查结果:
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
| 居民(户) | 1 | 2 | 3 | 4 |
| 月用电量(度/户) | 30 | 42 | 50 | 51 |
| A. | 中位数是50 | B. | 众数是51 | C. | 方差是42 | D. | 极差是21 |
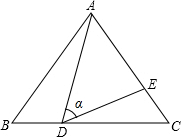 如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且$cosa=\frac{4}{5}$.下列结论:
如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且$cosa=\frac{4}{5}$.下列结论: