Question

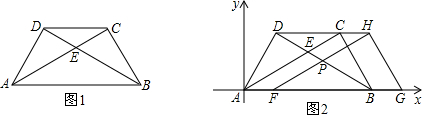
四边形ABCD是正方形．
（1）如图1，点G是BC边上任意一点（不与B、C两点重合），连接AG，作BF⊥AG于点F，DE⊥AG于点E．求证：△ABF≌△DAE；
（2）在（1）中，线段EF与AF、BF的等量关系是

 

（直接写出结论即可，不需要证明）；
（3）如图2，点G是CD边上任意一点（不与C、D两点重合），连接AG，作BF⊥AG于点F，DE⊥AG于点E．那么图中全等三角形是

 

，线段EF与AF、BF的等量关系是

 

（直接写出结论即可，不需要证明）．

Answer 1

分析：（1）根据正方形的性质可知：△ABF≌△ADE；
（2）利用全等三角形的性质，AE=BF，AF=DE，得出AF-BF=EF；
（3）同理可得出图（2），△ABF≌△DAE，EF=BF-AF．

解答：（1）证明：在正方形ABCD中，AB=AD，∠BAD=90°，
∴∠BAF+∠DAE=90°．
在Rt△ABF中，∠BAF+∠ABF=90°，
∴∠ABF=∠DAE．
在△ABF与△DAE中

∠ABF=∠DAE ∠AFB=∠DEA=90° AB=DA

，
∴△ABF≌△DAE（AAS）．

（2）解：EF=AF-BF．
∵△ABF≌△DAE，
∴AE=BF，
∵EF=AF-AE，
∴EF=AF-BF．

（3）解：△ABF≌△DAE．EF=BF-AF．
证明：在正方形ABCD中，AB=AD，∠BAD=90°，
∴∠BAF+∠DAE=90°．
在Rt△ABF中，∠BAF+∠ABF=90°，
∴∠ABF=∠DAE．
在△ABF与△DAE中

∠ABF=∠DAE ∠AFB=∠DEA=90° AB=DA

，
∴△ABF≌△DAE（AAS）．
∴AE=BF，
∴EF=AE-AF=BF-AF．

点评：主要考查了正方形的性质和全等三角形的判定．充分利用正方形的特殊性质来找到全等的条件，从而判定全等后利用全等三角形的性质解题．