题目内容
函数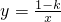 的图象与直线y=x没有交点,那么k的取值范围是________.
的图象与直线y=x没有交点,那么k的取值范围是________.
k>1
分析:函数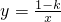 的图象与直线y=x没有交点,根据正比例函数及反比例函数的性质作答即可.
的图象与直线y=x没有交点,根据正比例函数及反比例函数的性质作答即可.
解答:直线y=x中,k=1>0,
∴过一、三象限,
要使两个函数没交点,
那么函数y= 的图象必须位于二、四象限,
的图象必须位于二、四象限,
那么1-k<0,
∴k>1.
故答案为:k>1.
点评:本题考查了反比例函数与一次函数的交点问题,难度不大,关键是结合函数图象解答较为简单.
分析:函数
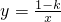 的图象与直线y=x没有交点,根据正比例函数及反比例函数的性质作答即可.
的图象与直线y=x没有交点,根据正比例函数及反比例函数的性质作答即可.解答:直线y=x中,k=1>0,
∴过一、三象限,
要使两个函数没交点,
那么函数y=
 的图象必须位于二、四象限,
的图象必须位于二、四象限,那么1-k<0,
∴k>1.
故答案为:k>1.
点评:本题考查了反比例函数与一次函数的交点问题,难度不大,关键是结合函数图象解答较为简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
两位同学在描述同一反比例函数的图象时,甲同学说:这个反比例函数的图象上任意一点到两坐标轴的距离的积都是3;乙同学说:这个反比例函数的图象与直线y=x有两个交点,你认为这两位同学所描述的反比例函数的解析式是( )
A、y=
| ||||
B、y=-
| ||||
C、y=-
| ||||
D、y=
|
两位同学在描述同一反比例函数的图象时,甲同学说:这个反比例函数图象上任意一点到两坐标轴距离的积都是2;乙同学说:这个反比例函数的图象与直线y=-2x有两个交点.你认为这两位同学所描述的反比例函数y与x的关系式为( )
A、y=-
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=-
|
 轴于N,且S△MON=6
轴于N,且S△MON=6