题目内容
在3×3的方格纸中，点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上，
（1）从A、D、E、F四点中任意取一点，以所取的这一点及点B、C为顶点画三角形，则所画三角形是等腰三角形的概率是 ；
（2）从A、D、E、F四点中先后任意取两个不同的点，以所取的这两点及点B、C为顶点画四边形，求所画四边形是平行四边形的概率（用树形图或列表法求解）
（1）
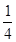；（2）
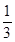
解析试题分析：（1）根据从A、D、E、F四点中任意取一点，只有点D可以与点B、C组成等腰三角形即可求得结果；
（2）先画树状图表示出所有可能的情况数，再根据概率公式求解即可.
（1）由图可得所画三角形是等腰三角形的概率是；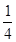
（2）画树状图表示出所有可能的情况如图所示：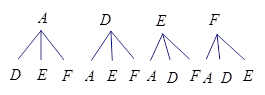
则所画四边形是平行四边形的概率是.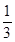
考点：基本作图，等腰三角形的性质，概率的求法
点评：解题的关键是熟练掌握概率的求法：概率=所求情况数与总情况数的比值.
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
23、在如图的方格纸中（每个小方格的边长都是1个单位）有一点O和△ABC．
在如图的方格纸中有一个菱形ABCD（A、B、C、D四点均为格点），若方格纸中每个最小正方形的边长为1，则该菱形的面积为
画图计算：
如图，在10*10的方格纸中，有一个格点四边形ABCD（即四边形的顶点都在格点上），在给出的方格纸上，画出四边形ABCD关于直线L的对称的四边形A1B1C1D1．
作图题：
作轴反射得到△A2B2C2，请在所给的方格纸中依次作出△A1B1C1和△A2B2C2．