Question

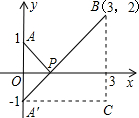
画图计算：
（1）在8×8的方格纸中画出△ABC关于点O的对称图形△A'B'C'，并在所画图中标明字母．
（2）设小方格的边长为1，求△A'B'C'中B'C'边上的高h的值．

Answer 1

分析：（1）连接三角形三点与O的连线，并延长相同单位，得到三点的对应点，顺次连接即可．
（2）根据三角形的边长，可以判定△ABC为直角三角形，继而求出B'C'边上的高h的值．

解答：解：（1）所作图形如下所示：


（2）由题意得：AB=

5

，AC=

20

=2

5

，BC=5，
∴△ABC为直角三角形．
△ABC的面积=

1

2

×

5

×2

5

=

1

2

×5×h，
解得：h=2．

点评：本题考查了轴对称变换作图，用到的知识点还有三角形面积的求法，作中心对称图形的关键是找到关键点的对应点．