ĖâÄŋÄÚČÝ
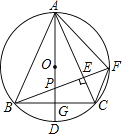
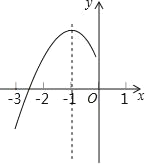
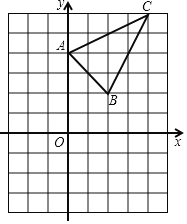
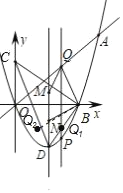
ĄūĖâÄŋĄŋČįÍžĢŽđýĩãAĢĻ5ĢŽ![]() ĢĐĩÄÅŨÎïÏßyĢ―ax2+bxĩÄķÔģÆÖáĘĮxĢ―2ĢŽĩãBĘĮÅŨÎïÏßÓëxÖáĩÄŌŧļö―ŧĩãĢŽĩãCÔÚyÖáÉÏĢŽĩãDĘĮÅŨÎïÏßĩÄķĨĩãĢŪ
ĢĐĩÄÅŨÎïÏßyĢ―ax2+bxĩÄķÔģÆÖáĘĮxĢ―2ĢŽĩãBĘĮÅŨÎïÏßÓëxÖáĩÄŌŧļö―ŧĩãĢŽĩãCÔÚyÖáÉÏĢŽĩãDĘĮÅŨÎïÏßĩÄķĨĩãĢŪ
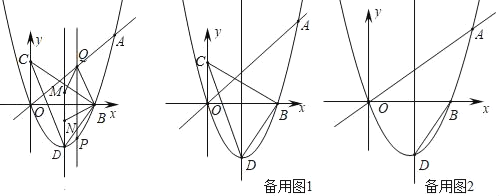
ĢĻ1ĢĐĮóaĄĒbĩÄÖĩĢŧ
ĢĻ2ĢĐĩąĄũBCDĘĮÖą―ĮČý―ĮÐÎĘąĢŽĮóĄũOBCĩÄÃæŧýĢŧ
ĢĻ3ĢĐÉčĩãPÔÚÖąÏßOAÏ·―ĮŌÔÚÅŨÎïÏßyĢ―ax2+bxÉÏĢŽĩãMĄĒNÔÚÅŨÎïÏßĩÄķÔģÆÖáÉÏĢĻĩãMÔÚĩãNĩÄÉÏ·―ĢĐĢŽĮŌMNĢ―2ĢŽđýĩãPŨũyÖáĩÄÆ―ÐÐÏß―ŧÖąÏßOAÓÚĩãQĢŽĩąPQŨîīóĘąĢŽĮëÖą―ÓÐīģöËÄąßÐÎBQMNĩÄÖÜģĪŨîÐĄĘąĩãQĄĒMĄĒNĩÄŨøąęĢŪ
Ąūīð°ļĄŋĢĻ1ĢĐ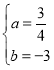 ĢĻ2ĢĐĩąĄũBDCΊֹ―ĮČý―ĮÐÎĘąĢŽĄũOBCĩÄÃæŧýĘĮ
ĢĻ2ĢĐĩąĄũBDCΊֹ―ĮČý―ĮÐÎĘąĢŽĄũOBCĩÄÃæŧýĘĮ![]() ŧō
ŧō![]() ĢŧĢĻ3ĢĐĩãQĄĒMĄĒNĩÄŨøąę·ÖąðΊ
ĢŧĢĻ3ĢĐĩãQĄĒMĄĒNĩÄŨøąę·ÖąðΊ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŪ
ĢŪ
Ąū―âÎöĄŋ
ĢĻ1ĢĐ°ŅĩãAĩÄŨøąęīúČëšŊĘý―âÎöĘ―ĢŽĀûÓÃķÔģÆÖá·―ģĖĢŽÁŠÁĒ·―ģĖŨéĢŽ―â·―ģĖŨéĮóĩÃaĄĒbĩÄÖĩ;
ĢĻ2ĢĐÉčĩãCĩÄŨøąęĘĮĢĻ0ĢŽmĢĐĢŪÓÉÓÚÃŧÓÐÖļÃũÖą―ĮĄũBCDÖÐĩÄÖą―ĮĢŽËųŌÔÐčŌŠ·ÖĀāĖÖÂÛĢšĩąĄÏCBD=90ĄãĄĒĄÏCDB=90ĄãĄĒĄÏBCD=90ĄãĘąĢŽĀûÓÃđīđÉķĻĀíÁÐģöđØÓÚmĩÄ·―ģĖĢŽÍĻđý―â·―ģĖĮóĩÃmĩÄÖĩĢŧČŧšóĀûÓÃČý―ĮÐÎĩÄÃæŧýđŦĘ――âīðĢŧ
ĢĻ3ĢĐĀûÓÃīýķĻÏĩĘý·ĻČ·ķĻÖąÏßOA―âÎöĘ―ÎŠ![]() ĢŪÓÉÅŨÎïÏßÉÏĩãĩÄŨøąęĖØÕũšÍÁ―ĩãžäĩÄūāĀëđŦĘ―ĮóĩÃĢšPQĢ―
ĢŪÓÉÅŨÎïÏßÉÏĩãĩÄŨøąęĖØÕũšÍÁ―ĩãžäĩÄūāĀëđŦĘ―ĮóĩÃĢšPQĢ―![]() x(
x(![]() x23x)Ģ―
x23x)Ģ―![]() x2+
x2+![]() xĢ―
xĢ―![]() (x
(x![]() )2+
)2+![]() ĢŽËųŌÔĀûÓÃķþīΚŊĘýŨîÖĩĩÄĮóĩÃÍÆÖŠĢšĩąPQŨîīóĘąĢŽÏßķÎBQΊķĻģĪĢŪÓÖŌōΊMN=2ĢŽËųŌÔŌŠĘđËÄąßÐÎBQMNĩÄÖÜģĪŨîÐĄĢŽÖŧÐčQM+BNŨîÐĄĢŪĀûÓÃÖáķÔģÆ-ŨîķĖ·ūķÎĘĖâĩÃĩ―ĩãQĢŪŨîšóĀûÓ÷―ģĖËžÏë―âīðĢŪ
ĢŽËųŌÔĀûÓÃķþīΚŊĘýŨîÖĩĩÄĮóĩÃÍÆÖŠĢšĩąPQŨîīóĘąĢŽÏßķÎBQΊķĻģĪĢŪÓÖŌōΊMN=2ĢŽËųŌÔŌŠĘđËÄąßÐÎBQMNĩÄÖÜģĪŨîÐĄĢŽÖŧÐčQM+BNŨîÐĄĢŪĀûÓÃÖáķÔģÆ-ŨîķĖ·ūķÎĘĖâĩÃĩ―ĩãQĢŪŨîšóĀûÓ÷―ģĖËžÏë―âīðĢŪ
―âĢšĢĻ1ĢĐĄßđýĩãA(5ĢŽ ![]() )ĩÄÅŨÎïÏßyĢ―ax2+bxĩÄķÔģÆÖáĘĮxĢ―2ĢŽ
)ĩÄÅŨÎïÏßyĢ―ax2+bxĩÄķÔģÆÖáĘĮxĢ―2ĢŽ
Ąā ĢŽ
ĢŽ
―âÖŪĢŽĩÃ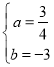 Ģŧ
Ģŧ
ĢĻ2ĢĐÉčĩãCĩÄŨøąęĘĮĢĻ0ĢŽmĢĐĢŪÓÉĢĻ1ĢĐŋÉĩÃÅŨÎïÏß![]() ĢŽ
ĢŽ
ĄāÅŨÎïÏßĩÄķĨĩãDĩÄŨøąęĘĮĢĻ2ĢŽĐ3ĢĐĢŽĩãBĩÄŨøąęĘĮĢĻ4ĢŽ0ĢĐĢŪ
ĩąĄÏCBDĢ―90ĄãĘąĢŽÓÐBC2+BD2Ģ―CD2ĢŪ
Ąā![]() ĢŽ
ĢŽ
―âÖŪĢŽĩÃ![]() ĢŽ
ĢŽ
Ąā![]() Ģŧ
Ģŧ
ĩąĄÏCDBĢ―90ĄãĘąĢŽÓÐCD2+BD2Ģ―BC2ĢŪ
Ąā![]() ĢŽ
ĢŽ
―âÖŪĢŽĩÃ![]() ĢŽ
ĢŽ
Ąā![]() Ģŧ
Ģŧ
ĩąĄÏBCDĢ―90ĄãĘąĢŽÓÐCD2+BC2Ģ―BD2ĢŪ
Ąā![]() ĢŽīË·―ģĖÎÞ―âĢŪ
ĢŽīË·―ģĖÎÞ―âĢŪ
ŨÛÉÏËųĘöĢŽĩąĄũBDCΊֹ―ĮČý―ĮÐÎĘąĢŽĄũOBCĩÄÃæŧýĘĮ![]() ŧō
ŧō![]() Ģŧ
Ģŧ
ĢĻ3ĢĐÉčÖąÏßyĢ―kxđýĩãA(5ĢŽ ![]() )ĢŽŋÉĩÃÖąÏß
)ĢŽŋÉĩÃÖąÏß![]() ĢŪ
ĢŪ
ÓÉĢĻ1ĢĐŋÉĩÃÅŨÎïÏß![]() ĢŽ
ĢŽ
ĄāPQ=![]() x(
x(![]() x23x)Ģ―
x23x)Ģ―![]() x2+
x2+![]() xĢ―
xĢ―![]() (x
(x![]() )2+
)2+![]() ĢŽ
ĢŽ
Ąāĩąx=![]() ĘąĢŽPQŨîīóĢŽīËĘąQĩãŨøąęĘĮ
ĘąĢŽPQŨîīóĢŽīËĘąQĩãŨøąęĘĮ![]() ĢŪ
ĢŪ
ĄāPQŨîīóĘąĢŽÏßķÎBQΊķĻģĪĢŪ
ĄßMNĢ―2ĢŽ
ĄāŌŠĘđËÄąßÐÎBQMNĩÄÖÜģĪŨîÐĄĢŽÖŧÐčQM+BNŨîÐĄĢŪ
―ŦĩãQÏōÏÂÆ―ŌÆ2ļöĩĨÎŧģĪķČĢŽĩÃĩã![]() ĢŽŨũĩã
ĢŽŨũĩã![]() đØÓÚÅŨÎïÏßĩÄķÔģÆÖáĩÄķÔģÆĩã
đØÓÚÅŨÎïÏßĩÄķÔģÆÖáĩÄķÔģÆĩã![]() ĢŽÖąÏßBQ2ÓëķÔģÆÖáĩÄ―ŧĩãūÍĘĮ·ûšÏĖõžþĩÄĩãNĢŽīËĘąËÄąßÐÎBQMNĩÄÖÜģĪŨîÐĄĢŪ
ĢŽÖąÏßBQ2ÓëķÔģÆÖáĩÄ―ŧĩãūÍĘĮ·ûšÏĖõžþĩÄĩãNĢŽīËĘąËÄąßÐÎBQMNĩÄÖÜģĪŨîÐĄĢŪ
ÉčÖąÏßyĢ―cx+dđýĩã![]() šÍĩãBĢĻ4ĢŽ0ĢĐĢŽ
šÍĩãBĢĻ4ĢŽ0ĢĐĢŽ
Ôō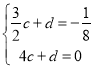 ,
,
―âÖŪĢŽĩÃ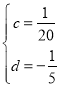 ,
,
ĄāÖąÏß![]() đýĩãQ2šÍĩãBĢŪ
đýĩãQ2šÍĩãBĢŪ
―â·―ģĖŨé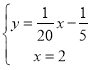 ĩÃ
ĩÃ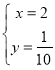 ,
,
ĄāĩãNĩÄŨøąęΊ![]() ĢŽĄāĩãMĩÄŨøąęΊ
ĢŽĄāĩãMĩÄŨøąęΊ![]() ĢŽ
ĢŽ
ËųŌÔĩãQĄĒMĄĒNĩÄŨøąę·ÖąðΊ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŪ
ĢŪ

 ―ĖēÄČŦ―âŨÖīĘūäÆŠÏĩÁÐīð°ļ
―ĖēÄČŦ―âŨÖīĘūäÆŠÏĩÁÐīð°ļ