题目内容
已知矩形纸片ABCD中,AB=2,BC=3.
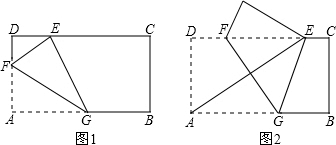
操作:将矩形纸片沿EF折叠,使点B落在边CD上.
【小题1】如图1,若点B与点D重合,你认为△EDA1和△FDC全等吗?如果全等,请给出证明,如果不全等,请说明理由
【小题2】如图2,若点B与CD的中点重合,请你判断△FCB1、△B1DG和△EA1G之间的关系,如果全等,只需写出结果,如果相似,请写出结果和相应的相似比
【小题3】如图2,请你探索,当点B落在CD边上何处,即B1C的长度为多少时,△FCB1与△B1DG全等.
【小题1】全等.-------------------------1分
证明:∵四边形ABCD是矩形,
所以∠A=∠B=∠C=∠ADC=90°,AB=CD,
由题意知:∠A=∠A1,∠B=∠A1DF=90°,CD=A1D,------------2分
所以∠ =∠C=90°,∠CDF+∠EDF=90°,---------------------3分
=∠C=90°,∠CDF+∠EDF=90°,---------------------3分
所以∠ DE=∠CDF,
DE=∠CDF,
所以△ED ≌△FDC(ASA).---------4分
≌△FDC(ASA).---------4分
【小题2】△B1DG和△EA1G全等.------------6分
△FCB1与△B1DG相似,设FC= ,
,
则B1F=BF= ,B1C=
,B1C= DC=1,
DC=1,
所以 ,所以
,所以 ,
,
所以△FCB1与△B1DG相似,相似比为4:3.----------------------9分
【小题3】△FCB1与△B1DG全等.设 ,则有
,则有 ,
, ,
,
在直角 中,可得
中,可得 ,整理得
,整理得 ,解得
,解得 (另一解舍去),
(另一解舍去),
所以,当B1C= 时,△FCB1与△B1DG全等.-----------------12分
时,△FCB1与△B1DG全等.-----------------12分
解析

练习册系列答案
相关题目
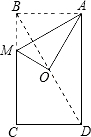 如图,已知矩形纸片ABCD中,AD=6,AB=a(a<6),在BC边上取一点M,将△ABM沿AM折叠后点B恰好落在矩形ABCD的对称中心O处,则a的值为
如图,已知矩形纸片ABCD中,AD=6,AB=a(a<6),在BC边上取一点M,将△ABM沿AM折叠后点B恰好落在矩形ABCD的对称中心O处,则a的值为