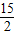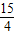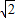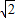Question

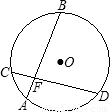
(2003·重庆)如图所示，△ABP与△CDP是两个全等的等边三角形，且PA⊥PD有下列四个命题：①；②AD∥BC；③直线PC与AB垂直；④四边形ABCD是轴对称图形．其中正确结论的个数为

[　　]

A．1

B．2

C．3

D．4

Answer 1

答案：D
解析：

解　∵△ABP与△CDP是两个全等的等边三角形，∴PB=PC，∠APB=∠ABP=∠BAP=∠DCP=∠DCP=∠CDP=． 　　∵∠APD=，∴∠BPC=．∴∠PBC=．∴①正确； 　　∵∠PAD=∠PDA=， 　　∴∠BAD=∠BAP＋∠PAD=． 　　而∠ABC=∠ABP＋∠PBC=， 　　∴∠BAD＋∠ABC=． 　　∴AD∥BC．∴②正确； 　　延长CP交AB于点E， 　　∵∠CBA＋∠ABC=． 　　∴AD∥BC．②正确； 　　延长CP交AB于点E， 　　∵∠CBA＋∠PCB=， 　　∴CEB＝．∴PC⊥AB． 　　∴③正确； 　　∵AD∥BC，AB=CD， 　　∴四边形ABCD是等腰梯形， 　　∴四边形ABCD是轴对称图形， 　　∴④正确，共有四个命题正确．故选D．