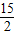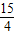题目内容
（2003•重庆）如图，⊙O中弦AB、CD相交于点F，AB=10，AF=2．若CF：DF=1：4，则CF的长等于（ ）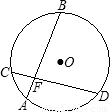
A．
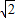
B．2
C．3
D．2
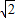
【答案】分析：根据相交弦定理“圆内两弦相交于圆内一点，各弦被这点所分得的两线段的长的乘积相等”进行计算．
解答：解：∵CF：DF=1：4
∴DF=4CF
又AB=10，AF=2
∴BF=10-2=8
由相交弦定理得：FA•FB=FC•FD
即2×8=FC×4FC
解得FC=2．
故选B．
点评：本题主要考查相交弦定理“圆内两弦相交于圆内一点，各弦被这点所分得的两线段的长的乘积相等”的应用．
解答：解：∵CF：DF=1：4
∴DF=4CF
又AB=10，AF=2
∴BF=10-2=8
由相交弦定理得：FA•FB=FC•FD
即2×8=FC×4FC
解得FC=2．
故选B．
点评：本题主要考查相交弦定理“圆内两弦相交于圆内一点，各弦被这点所分得的两线段的长的乘积相等”的应用．
练习册系列答案
阶梯计算系列答案
相关题目
