题目内容
【题目】阅读材料:类比是数学中常用的数学思想.比如,我们可以类比多位数的加、减、乘、除的竖式运算方法,得到多项式与多项式的加、减、乘、除的运算方法.
例:
①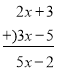 ②
②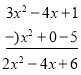
![]()
![]()
③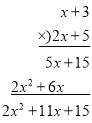 ④
④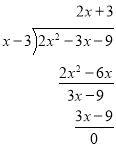
![]()
![]()
理解应用:
(1)请仿照上面的竖式方法计算:![]() ;
;
(2)已知两个多项式的和为![]() ,其中一个多项式为
,其中一个多项式为![]() ,请用竖式的方法求出另一个多项式.
,请用竖式的方法求出另一个多项式.
(3)已知一个长为![]() ,宽为
,宽为![]() 的矩形
的矩形![]() ,将它的长增加
,将它的长增加![]() ,宽增加
,宽增加![]() 得到一个新矩形
得到一个新矩形![]() ,且矩形
,且矩形![]() 的周长是矩形
的周长是矩形![]() 周长的
周长的![]() 倍(如图).同时,矩形
倍(如图).同时,矩形![]() 的面积和另一个边长为
的面积和另一个边长为![]() 的矩形
的矩形![]() 的面积相等,求
的面积相等,求![]() 的值和矩形
的值和矩形![]() 的另一边长.
的另一边长.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)m=-8,矩形C的另一边长为5x-10.
;(3)m=-8,矩形C的另一边长为5x-10.
【解析】
(1)根据多项式与多项式的乘法竖式的运算方法计算即可求解;
(2)根据多项式与多项式的减法竖式的运算方法计算即可求解;
(3)根据已知条件,求出面积,然后分解多项式即可.
解:(1)
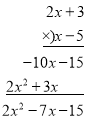
(2x+3)(x5)=2x27x15
(2)
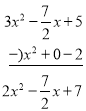
另一个多项式为:2x2![]() x+7
x+7
(3)∵矩形B的周长是A周长的3倍
∴2×(x+2+x2)×3=2×(x+10+x2+a)
∴a=4x8
所以矩形B的面积为:(x+8)(5x10)=5x2+30x80
矩形C的面积与B的面积相等,5x2+30x80=(x+8)(5x10),
故m=8,矩形C的另一边为5x10.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目