题目内容
20. 如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF,BF,DF.
如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF,BF,DF.(1)求证:△ABC≌△ABF;
(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给予证明.
分析 (1)首先利用平行线的性质得到∠FAB=∠CAB,然后利用SAS证得两三角形全等即可;
(2)当∠CAB=60°时,四边形ADFE为菱形,根据∠CAB=60°,得到∠FAB=∠CAB=∠CAB=60°,从而得到EF=AD=AE,利用邻边相等的平行四边形是菱形进行判断四边形ADFE是菱形.
解答 解:(1)证明:∵EF∥AB,
∴∠E=∠CAB,∠EFA=∠FAB,
∵∠E=∠EFA,
∴∠FAB=∠CAB,
在△ABC和△ABF中,
$\left\{\begin{array}{l}{AF=AC}\\{∠FAB=∠CAB}\\{AB=AB}\end{array}\right.$,
∴△ABC≌△ABF;
(2)当∠CAB=60°时,四边形ADFE为菱形.
证明:∵∠CAB=60°,
∴∠FAB=∠CAB=∠CAB=60°,
∴EF=AD=AE,
∴四边形ADFE是菱形.
点评 本题考查了菱形的判定、全等三角形的判定与性质及圆周角定理的知识,解题的关键是了解菱形的判定方法及全等三角形的判定方法,难度不大.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
5. 如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )
如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )
 如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )
如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )| A. | 50° | B. | 30° | C. | 20° | D. | 15° |
12. 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为( )
 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为( )| A. | 26° | B. | 36° | C. | 46° | D. | 56° |
9.在“青春脉动•唱响黔南校园青年歌手大赛”总决赛中,7位评委对某位选手评分为(单位:分):9、8、9、7、8、9、7.这组数据的众数和平均数分别是( )
| A. | 9、8 | B. | 9、7 | C. | 8、7 | D. | 8、8 |

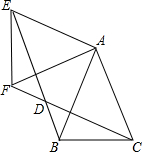 如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D. 甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论: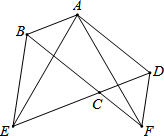 如图,在?ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.
如图,在?ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.