题目内容
有一边长为2的正方形纸片ABCD，先将正方形ABCD对折，设折痕为EF（如图①）；再沿
过点D的折痕将角A翻折，使得点A落在EF的H上（如图②），折痕交AE于点G，则EG的长度为
- A.4
-6 - B.2-3
- C.8-4
- D.4-2
B
分析：观察图形，利用正方形性质，勾股定理，三角函数等知识即可解答．
解答：本题可通过用EG表示EH，然后通过EF的长来求EG．
∵∠GHD=90°
∴∠EHG+∠DHF=90°
∵∠EGH+∠EHG=90°
∴∠EGH=∠DHF
Rt△HDF中，HD=2，DF=1
根据勾股定理可得出：FH=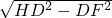
=
sin∠DHF=DF：DH=1：2，因此∠DHF=30°
Rt△EGH中，设EG=x，EH=EG•tan∠EGH=x•tan30°=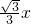
因为EF=EH+HF=+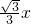=2，x=2-3，故选B．
点评：本题综合考查了正方形的性质，勾股定理，三角函数等知识点．
分析：观察图形，利用正方形性质，勾股定理，三角函数等知识即可解答．
解答：本题可通过用EG表示EH，然后通过EF的长来求EG．
∵∠GHD=90°
∴∠EHG+∠DHF=90°
∵∠EGH+∠EHG=90°
∴∠EGH=∠DHF
Rt△HDF中，HD=2，DF=1
根据勾股定理可得出：FH=
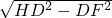=sin∠DHF=DF：DH=1：2，因此∠DHF=30°
Rt△EGH中，设EG=x，EH=EG•tan∠EGH=x•tan30°=
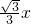
因为EF=EH+HF=
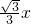+=2，x=2-3，故选B．点评：本题综合考查了正方形的性质，勾股定理，三角函数等知识点．
练习册系列答案
相关题目
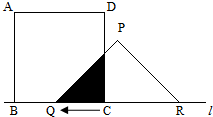头所示方向开始匀速运动，t秒后正方形ABCD与等腰△PQR重合部分的面积为Scm2．解答下列问题：
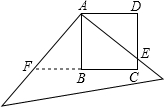如图：有一边长为5cm的正方形塑料模板ABCD，将一块足够大的直角三角板的直角顶点落在点A，两直角边与CD交于点E，与CB的延长线交于点F，则四边形AECF的面积为