题目内容
已知x1,x2是一元二次方程x2+3x+1=0的两个实数根,则x12+x22= .
考点:根与系数的关系
专题:计算题
分析:根据根与系数的关系得到得x1+x2=-3,x1x2=1,再利用完全平方公式变形得到x12+x22=(x1+x2)2-2x1x2,然后利用整体代入的方法计算.
解答:解:根据题意得x1+x2=-3,x1x2=1,
所以x12+x22=(x1+x2)2-2x1x2=(-3)2-2×1=7.
故答案为7.
所以x12+x22=(x1+x2)2-2x1x2=(-3)2-2×1=7.
故答案为7.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
在-(-8),-|-1|,-|0|,+(-3),-|+5|,-a这些数中,一定是负数的个数有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
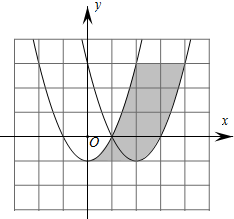 如图,7×8网格的每个小正方形边长均为1,将抛物线y1=x2-1的图象向右平移2个单位得到抛物线y2.
如图,7×8网格的每个小正方形边长均为1,将抛物线y1=x2-1的图象向右平移2个单位得到抛物线y2.