题目内容
如图，将长方形ABCD沿EF折叠，使CD落在GH的位置，GH交BC于M，若∠HMB=52°，则∠HEF的度数为71°
71°
．分析：首先根据折叠可得：∠HEF=∠FED，再证明∠AEH=∠MFG=90°-52°=38°，然后可得∠HEF的度数．
解答：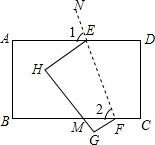
解：延长FE，
由折叠可得：∠HEF=∠FED，
∵AE∥BC，
∴∠1=∠2，
∵HE∥GF，
∴∠NEH=∠EFG，
∴∠AEH=∠MFG，
∵∠HMB=∠FMG，
∴∠MFG=90°-∠FMG=90°-∠HMB=38°，
∴∠AEH=38°，
∴∠HEF=（180°-∠AEH）÷2=71°．
故答案为：71°．
解：延长FE，由折叠可得：∠HEF=∠FED，
∵AE∥BC，
∴∠1=∠2，
∵HE∥GF，
∴∠NEH=∠EFG，
∴∠AEH=∠MFG，
∵∠HMB=∠FMG，
∴∠MFG=90°-∠FMG=90°-∠HMB=38°，
∴∠AEH=38°，
∴∠HEF=（180°-∠AEH）÷2=71°．
故答案为：71°．
点评：此题主要考查了图形的折叠变换，关键是掌握折叠的性质：折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．解题时要找到对应边和角．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
如图，将面积为a2的小正方形和面积为b2的大长方形放在一起（a＞0，b＞0），求三角形ABC的面积．
如图，将长方形ABCD沿对角线BD折叠，使点C恰好落在如图C′的位置，若∠DBC=15°，则∠ABC′=（ ）
如图，将长方形ABCD沿对角线AC剪开，得到两个三角形为△ABC和△DEF．若将△DEF经过不同的变换，使得△ABC和△DEF有一条边重合，这样得到的不同的三角形有
如图，将长方形ABCD沿对角线BD折叠，使点C恰好落在如图C′的位置，若∠DBC=15°，则∠ABC′=