题目内容
 如图,I为△ABC的内心,AI交△ABC的外接圆O于点D,交BC于点P,连接BD、BI、CI,则下列结论:
如图,I为△ABC的内心,AI交△ABC的外接圆O于点D,交BC于点P,连接BD、BI、CI,则下列结论:
①DI=DB;②DB2=DP•DA;③AB•AC=PA•PD;④∠BIC=90°+ ∠BOC.其中正确的个数有
∠BOC.其中正确的个数有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:根据I为△ABC的内心,得∠BAD=∠CAD,∠ABI=∠CBI,则 =
= ,根据同弧所对的圆周角相等即可得出∠CAD=∠CBD,再根据外角的性质得出∠DBI=∠DIB,则DI=DB;可证明△DBP∽△DAB,即可得出DB 2=DP•DA;可证明∠BIC=90°+
,根据同弧所对的圆周角相等即可得出∠CAD=∠CBD,再根据外角的性质得出∠DBI=∠DIB,则DI=DB;可证明△DBP∽△DAB,即可得出DB 2=DP•DA;可证明∠BIC=90°+ ∠BAC.从而得出∠BIC=90°+
∠BAC.从而得出∠BIC=90°+ ∠BOC.
∠BOC.
解答:∵I为△ABC的内心,∴∠BAD=∠CAD,∠ABI=∠CBI,
∴ =
= ,
,
∴∠CAD=∠CBD,
∵∠BID=∠BAD+∠ABI,∠DBI=∠DBP+∠PBI,
∴∠DBI=∠DIB,
∴DI=DB,故①正确;
∵△DBP∽△DAB,
∴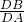 =
= ,
,
即DB2=DP•DA,故②正确;
根据相交弦定理,得PB•PC=PA•PD,而△ABP与△ACP一定不相似,
∴AB•AC=PA•PD不成立,故③不正确;
∵∠BIC=90°+ ∠BAC,∠BOC=2∠BAC,
∠BAC,∠BOC=2∠BAC,
∴∠BIC=90°+ ∠BOC.故④正确.
∠BOC.故④正确.
故选C.
点评:本题考查了三角形的内切圆以及相似三角形的判定和性质,是基础知识要熟练掌握.
分析:根据I为△ABC的内心,得∠BAD=∠CAD,∠ABI=∠CBI,则
 =
= ,根据同弧所对的圆周角相等即可得出∠CAD=∠CBD,再根据外角的性质得出∠DBI=∠DIB,则DI=DB;可证明△DBP∽△DAB,即可得出DB 2=DP•DA;可证明∠BIC=90°+
,根据同弧所对的圆周角相等即可得出∠CAD=∠CBD,再根据外角的性质得出∠DBI=∠DIB,则DI=DB;可证明△DBP∽△DAB,即可得出DB 2=DP•DA;可证明∠BIC=90°+ ∠BAC.从而得出∠BIC=90°+
∠BAC.从而得出∠BIC=90°+ ∠BOC.
∠BOC.解答:∵I为△ABC的内心,∴∠BAD=∠CAD,∠ABI=∠CBI,
∴
 =
= ,
,∴∠CAD=∠CBD,
∵∠BID=∠BAD+∠ABI,∠DBI=∠DBP+∠PBI,
∴∠DBI=∠DIB,
∴DI=DB,故①正确;
∵△DBP∽△DAB,
∴
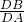 =
= ,
,即DB2=DP•DA,故②正确;
根据相交弦定理,得PB•PC=PA•PD,而△ABP与△ACP一定不相似,
∴AB•AC=PA•PD不成立,故③不正确;
∵∠BIC=90°+
 ∠BAC,∠BOC=2∠BAC,
∠BAC,∠BOC=2∠BAC,∴∠BIC=90°+
 ∠BOC.故④正确.
∠BOC.故④正确.故选C.
点评:本题考查了三角形的内切圆以及相似三角形的判定和性质,是基础知识要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
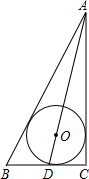 如图,⊙O为△ABC的内切圆,∠C=90度,OA的延长线交BC于点D,AC=4,CD=1,则⊙O的半径等于( )
如图,⊙O为△ABC的内切圆,∠C=90度,OA的延长线交BC于点D,AC=4,CD=1,则⊙O的半径等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
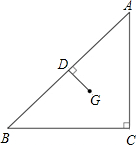 如图,G为△ABC的重心,其中∠C=90°,D在AB上,GD⊥AB.若AB=29,AC=20,BC=21,则GD的长度为何?( )
如图,G为△ABC的重心,其中∠C=90°,D在AB上,GD⊥AB.若AB=29,AC=20,BC=21,则GD的长度为何?( )| A、7 | ||
B、14
| ||
C、
| ||
D、
|
 6、如图,⊙O为△ABC的外接圆,BC为直径,AC=AB,则∠D的度数为( )
6、如图,⊙O为△ABC的外接圆,BC为直径,AC=AB,则∠D的度数为( ) 25、如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,那么BE⊥AC吗?为什么?
25、如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,那么BE⊥AC吗?为什么?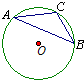 5、如图,⊙O为△ABC的外接圆,且∠A=30°,AB=8cm,BC=5cm,则⊙O的半径=
5、如图,⊙O为△ABC的外接圆,且∠A=30°,AB=8cm,BC=5cm,则⊙O的半径=