题目内容
?ABCD中,有两个内角的度数比为1:2,则?ABCD中较大的内角是
- A.90°
- B.60°
- C.120°
- D.45°
C
分析:由?ABCD中,有两个内角的度数比为1:2,可得此两角互补,继而求得答案.
解答:∵四边形ABCD是平行四边形,
∴对角相等,邻角互补,
∵有两个内角的度数比为1:2,
∴?ABCD中较大的内角是:180°×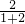 =120°.
=120°.
故选C.
点评:此题考查了平行四边形的性质.此题难度不大,注意掌握平行四边形对角相等,邻角互补.
分析:由?ABCD中,有两个内角的度数比为1:2,可得此两角互补,继而求得答案.
解答:∵四边形ABCD是平行四边形,
∴对角相等,邻角互补,
∵有两个内角的度数比为1:2,
∴?ABCD中较大的内角是:180°×
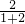 =120°.
=120°.故选C.
点评:此题考查了平行四边形的性质.此题难度不大,注意掌握平行四边形对角相等,邻角互补.

练习册系列答案
相关题目
 正方形ABCD中,有两个分别内接于△ABC,△ACD的小正方形,它们的面积分别为m,n(如图)则
正方形ABCD中,有两个分别内接于△ABC,△ACD的小正方形,它们的面积分别为m,n(如图)则 =
= 
 =
= 