Question

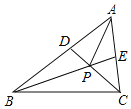
【题目】如图，△ABC中，AB＝AC．O是△ABC内一点，OD是AB的垂直平分线，OF⊥AC，且OD＝OF．

（1）当∠OAC＝27°时，求：∠OBC的度数．

（2）求证：AF＝CF．

Answer 1

【答案】（1）∠OBC＝36°；（2）见解析

【解析】

（1）由AB＝AC，可得∠ABC＝∠ACB， , ，由OD是AB的垂直平分线，得出OA＝OB，，然后根据∠OAC的度数求出∠ABC，∠ABO的度数，最后利用∠OBC＝∠ABC﹣∠ABO求解即可

（2）通过垂直平分线的性质和等腰三角形的性质证出OA=OC，然后通过HL证明，即可证出AF＝FC．

解：（1）连接AO，并延长交BC于点E，连接OB，OC，

∵AB＝AC，

∴∠ABC＝∠ACB，AO平分∠DAF，

,

∵OD是AB的垂直平分线，

∴OA＝OB，

∵∠OAC＝27°

∴∠BAC＝27°×2＝54°，

∴∠ABC＝∠ACB＝（180°﹣54°）＝63°，

∴∠OBC＝∠ABC﹣∠ABO＝63°﹣27°＝36°；

（2）∵OD是AB的垂直平分线，

∴OA＝OB，

又∵AB＝AC，

∴AE⊥BC，BE＝CE，

∴OE垂直平分BC，

∴OB＝OC，

∴OA＝OC，

∵OF⊥AC，

在和中，

∴

∴AF＝FC．