题目内容
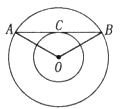
如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=120°,则大圆半径R与小圆半径r之间的关系满足

A.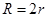 | B.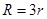 | C.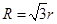 | D.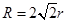 |
A.
试题分析:连接OC,

∵C为切点,
∴OC⊥AB,
∵OA=OB,
∴∠COB=
 ∠AOB=60°,
∠AOB=60°,∴∠B=30°,
∴OC=
 OB,
OB,∴R=2r.
故选A.
考点: 1.切线的性质;2.含30度角的直角三角形;3.垂径定理.

练习册系列答案
相关题目
题目内容

A.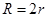 | B.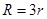 | C.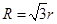 | D.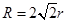 |

 ∠AOB=60°,
∠AOB=60°, OB,
OB,