题目内容
求出抛物线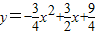
的最大值，并说明该抛物线是由哪一条形如y=ax2的抛物线经过怎样的变换得到的？
【答案】分析：先把抛物线
化为顶点式，即可求出最大值，根据上加下减，左加右减的平移原则即可说明该抛物线是由哪一条形如y=ax2的抛物线经过怎样的变换得到的．
解答：解：抛物线
，
y=-
（x-1）2+3，当x=1时，y取最大值为3，
故该抛物线是由y=-
x2经过向上平移3个单位得到y=-
x2+3，
再把y=-
x2+3中的x向右平移1个单位得到：y=-
（x-1）2+3．
点评：本题考查了二次函数的最值及二次函数图象与几何变换，难度一般，关键是掌握用配方法求最值和上加下减，左加右减的平移原则．
化为顶点式，即可求出最大值，根据上加下减，左加右减的平移原则即可说明该抛物线是由哪一条形如y=ax2的抛物线经过怎样的变换得到的．解答：解：抛物线
，y=-
（x-1）2+3，当x=1时，y取最大值为3，故该抛物线是由y=-
x2经过向上平移3个单位得到y=-x2+3，再把y=-
x2+3中的x向右平移1个单位得到：y=-（x-1）2+3．点评：本题考查了二次函数的最值及二次函数图象与几何变换，难度一般，关键是掌握用配方法求最值和上加下减，左加右减的平移原则．
练习册系列答案
阅读快车系列答案
相关题目
（2012•攀枝花）如图，在平面直角坐标系xOy中，四边形ABCD是菱形，顶点A、C、D均在坐标轴上，且AB=5，sinB=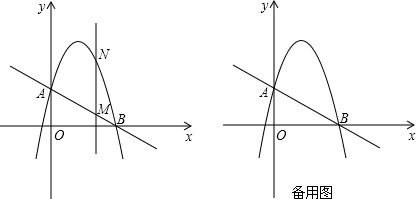
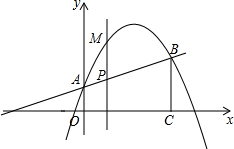如图，在平面直角坐标系中，已知抛物线y=-
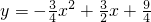的最大值，并说明该抛物线是由哪一条形如y=ax2的抛物线经过怎样的变换得到的？