Question

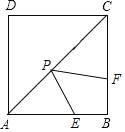
【题目】如图，正方形ABCD中，AB＝8，点E、F分别在边AB、BC上，BE＝BF＝2，点P是对角线AC上的一个动点，则PE+PF的最小值是_____．

Answer 1

【答案】4

【解析】

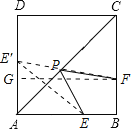
过E作AC的垂线交AD于点E′，连接E′F交AC于点P，过F作AD的垂线交AD于点G，则E′F即为所求，根据正方形的性质可知△AEE′是等腰三角形，AE′＝6，GA＝BF＝2，即可求出GE′的长，再由勾股定理即可求出E′F的长．

解：过E作AC的垂线交AD于点E′，连接E′F交AC于点P，过F作AD的垂线交AD于点G，则E′F即为所求，

∵四边形ABCD是正方形，

∴∠DAC＝∠BAC＝45°，

∵EE′⊥AC，

∴△AEE′是等腰三角形，

∴AE＝AE′＝8﹣2＝6，

∵GF⊥AD，

∴GA＝BF＝2，

∴GE′＝AE'﹣AG＝6﹣2＝4，

在Rt△GFE′中，GE′＝4，GF＝8，

∴E′F＝．

故答案为：.