题目内容
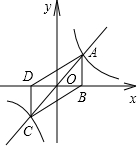 正比例函数y=
正比例函数y=| 1 |
| 2 |
| 2 |
| x |
分析:由于正比例函数y=
x与反比例函数y=
的图象关于原点对称,则A、C关于原点对称;可得OB=OD,于是S△AOB=S△AOD,根据反比例函数k的几何意义,求出S△AOB,即可得到四边形ABCD的面积.
| 1 |
| 2 |
| 2 |
| x |
解答:解:∵y=
x与反比例函数y=
的图象关于原点对称,
∴OB=OD,
∴S△AOD=S△AOB=2×
=1,
则四边形ABCD的面积为4.
故答案为:4.
| 1 |
| 2 |
| 2 |
| x |
∴OB=OD,
∴S△AOD=S△AOB=2×
| 1 |
| 2 |
则四边形ABCD的面积为4.
故答案为:4.
点评:本题考查了反比例函数系数k的几何意义,不仅要会计算k的值,还要理解反比例函数和正比例函数的对称性.

练习册系列答案
相关题目
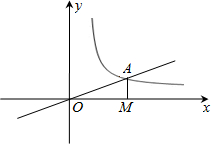 如图,正比例函数
如图,正比例函数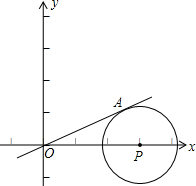 我们知道两个一次函数y=k1x+b1,y=k2x+b2,当k1=k2时,这两个一次函数的图象相互平行,那么两个一次函数的图象什么情况下相互垂直呢?下面我们就来探索.
我们知道两个一次函数y=k1x+b1,y=k2x+b2,当k1=k2时,这两个一次函数的图象相互平行,那么两个一次函数的图象什么情况下相互垂直呢?下面我们就来探索. 作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点.
作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点. 已知一次函数y1=kx+b的图象经过点(-1,-5)且与正比例函数y2=
已知一次函数y1=kx+b的图象经过点(-1,-5)且与正比例函数y2=