题目内容
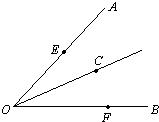 18、如图,已知点C是∠AOB平分线上一点,点E,F分别在边OA,OB上,如果要得到OE=OF,需要添加以下条件中的某一个即可,请你写出所有可能结果的序号为
18、如图,已知点C是∠AOB平分线上一点,点E,F分别在边OA,OB上,如果要得到OE=OF,需要添加以下条件中的某一个即可,请你写出所有可能结果的序号为①②④
①∠OCE=∠OCF;②∠OEC=∠OFC;③EC=FC;④EF⊥OC.分析:要得到OE=OF,就要让△OCE≌△OCF,①②④都行,只有③EC=FC不行,因为证明三角形全等没有边边角定理.
解答:解:①若①∠OCE=∠OCF,根据三角形角平分线的性质可得,∠EOC=∠COF,故居ASA定理可求出△OEC≌△OFC,由三角形全等的性质可知OE=OF.正确;
②若∠OEC=∠OFC,同①可得△OEC≌△OFC,由三角形全等的性质可知OE=OF.正确;
③若EC=FC条件不够不能得出.错误;
④若EF⊥OC,根据SSS定理可求出△OEC≌△OFC,由三角形全等的性质可知OE=OF.正确.
故填①②④.
②若∠OEC=∠OFC,同①可得△OEC≌△OFC,由三角形全等的性质可知OE=OF.正确;
③若EC=FC条件不够不能得出.错误;
④若EF⊥OC,根据SSS定理可求出△OEC≌△OFC,由三角形全等的性质可知OE=OF.正确.
故填①②④.
点评:本题主要考查了三角形全等的判与性质;由求线段相等转化为添加条件使三角形全等是正确解答本题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
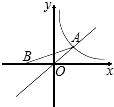 如图,已知点A是函数y=x与y=
如图,已知点A是函数y=x与y=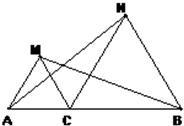 20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.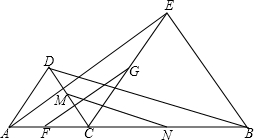 M、N分别是线段AC、CE、CD、CB的中点,
M、N分别是线段AC、CE、CD、CB的中点,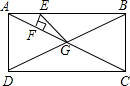 如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG=
如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG= 如图,已知点C是线段AD的中点,AC=15cm,BC=22cm,分别求线段AD和BD的长度.
如图,已知点C是线段AD的中点,AC=15cm,BC=22cm,分别求线段AD和BD的长度.